题目内容
【题目】(2015·新课标I卷)在直角坐标系xoy中,曲线C:y=![]() 与直线y=kx+a(a>0)交与M,N两点,
与直线y=kx+a(a>0)交与M,N两点,
(1)当k=0时,分别求C在点M和N处的切线方程;
(2)y轴上是否存在点P , 使得当k变动时,总有∠OPM=∠OPN?说明理由.
【答案】
(1)
![]() x-y-a=0或
x-y-a=0或![]() x+y+a=0
x+y+a=0
(2)
存在
【解析】
(I)由题设可得M(2![]() ,a), N(-2
,a), N(-2![]() ,a), 或M(-2
,a), 或M(-2![]() ,a), N(2
,a), N(2![]() ,a), ∵y'=
,a), ∵y'=![]() x, 故y=
x, 故y=![]() 在x=2
在x=2![]() a处的导数值为
a处的导数值为![]() ,C在(2
,C在(2![]() a,a)处的切线方程为y-a=
a,a)处的切线方程为y-a=![]() (x-2
(x-2![]() ), 即
), 即![]() x-y-a=0. 故y=
x-y-a=0. 故y=![]() 在x=-2
在x=-2![]() a处的导数值为-
a处的导数值为-![]() ,C在(-2
,C在(-2![]() a,a)处的切线方程为y-a=-
a,a)处的切线方程为y-a=-![]() (x+2
(x+2![]() ), 即
), 即![]() x+y+a=0。 故所求切线方程为
x+y+a=0。 故所求切线方程为![]() x-y-a=0或
x-y-a=0或![]() x+y+a=0。
x+y+a=0。
(II)存在符合题意的点,证明如下:
设P(0,b)为复合题意得点,M(x1,y1), N(x2,y2), 直线PM, PN的斜率分别为k1,k2, 将y=kx+a代入C得方程整理得x2-4kx-4a=0. ∴ x1+x2=4k, x1x2=-4a. ∴k1+k2=![]() =
=![]() =
=![]() . 当b=-a时,有k1+k2=0, 则直线PM的倾斜角与直线PN的倾斜角互补,故∠OPM=∠OPN,所以P(0,-a)符合题意。
. 当b=-a时,有k1+k2=0, 则直线PM的倾斜角与直线PN的倾斜角互补,故∠OPM=∠OPN,所以P(0,-a)符合题意。
【考点精析】认真审题,首先需要了解抛物线的参数方程(抛物线![]() 的参数方程可表示为
的参数方程可表示为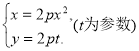 ).
).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目