题目内容
【题目】已知点![]() 与点
与点![]() 在直线
在直线![]() 的两侧,给出以下结论:①
的两侧,给出以下结论:① ![]() ;② 当
;② 当![]() 时,
时,![]() 有最小值,无最大值;③
有最小值,无最大值;③ ![]() ;④ 当
;④ 当![]() 且
且![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;正确的个数是( )
;正确的个数是( )
A.1B.2C.3D.4
【答案】B
【解析】
先由题意得到![]() ,推出
,推出![]() ,根据题意,作出不等式所表示的平面区域,分别由
,根据题意,作出不等式所表示的平面区域,分别由![]() ,
,![]() ,
,![]() 的几何意义,结合图像,即可得出结果.
的几何意义,结合图像,即可得出结果.
因为点![]() 与点
与点![]() 在直线
在直线![]() 的两侧,
的两侧,
所以![]() ,即
,即![]() ,故①错误;
,故①错误;
当![]() 时,
时,![]() 表示的平面区域如下:
表示的平面区域如下:
令![]() ,则
,则![]() ,显然
,显然![]() 表示直线
表示直线![]() 在
在![]() 轴截距的
轴截距的![]() 倍,
倍,
截距越大,![]() 越大;
越大;
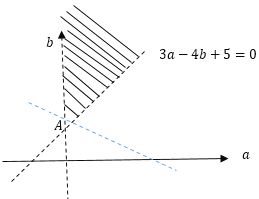
由图像可得,![]() 无最大值和最小值;故②错误.
无最大值和最小值;故②错误.
设坐标原点到直线![]() 的距离为
的距离为![]() ,则
,则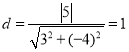 ,
,
又![]() 表示
表示![]() 对应的平面区域内的点与原点距离的平方,
对应的平面区域内的点与原点距离的平方,
因此![]() ;故③正确;
;故③正确;
因为![]() 表示
表示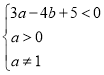 对应平面区域内的点
对应平面区域内的点![]() 与定点
与定点![]() 连线斜率,
连线斜率,
作出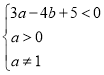 对应的平面区域如下:
对应的平面区域如下:
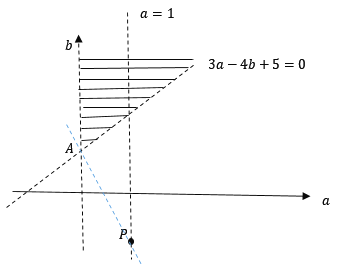
由图像可得: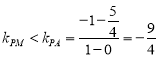 或
或![]() ,
,
即![]() 的取值范围是
的取值范围是![]() ,故④正确.
,故④正确.
故选:B

【题目】某手机生产企业为了解消费者对某款手机的认同情况,通过销售部随机抽取50名购买该款手机的消费者,并发出问卷调查(满分50分),该问卷只有20份给予回复,这20份的评分如下:
男 | 47,36,28,48,48,44,50,46,50,37,35,49 |
女 | 38,37,50,36,38,45,29,39 |
(1)完成下面的茎叶图,并求12名男消费者评分的中位数与8名女消费者评分的众数及平均值;
男 | 女 | |
2 | ||
3 | ||
4 | ||
5 |
满意 | 不满意 | 合计 | |
男 | |||
女 | |||
合计 |
(2)若大于40分为“满意”,否则为“不满意”,完成上面的![]() 列联表,并判断是否有95%的把握认为消费者对该款手机的“满意度”与性别有关;
列联表,并判断是否有95%的把握认为消费者对该款手机的“满意度”与性别有关;
(3)若从回复的20名消费者中按性别用分层抽样的方法抽取5人,再从这5人中随机抽取2人作进一步调查,求至少有1名女性消费者被抽到的概率.
附:
| 0.05 | 0.025 | 0.01 |
| 3.841 | 5.024 | 6.635 |
【题目】已知函数![]() 的定义域为
的定义域为![]() ,部分对应值如下表.
,部分对应值如下表.
x |
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
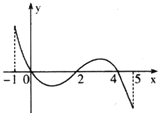
![]() 的导函数
的导函数![]() 的图象如图所示:下列关于
的图象如图所示:下列关于![]() 的命题:
的命题:
![]() 函数
函数![]() 是周期函数;
是周期函数;
![]() 函数
函数![]() 在
在![]() 是减函数;
是减函数;
![]() 如果当
如果当![]() 时,
时,![]() 的最大值是2,那么t的最大值为4;
的最大值是2,那么t的最大值为4;
![]() 函数
函数![]() 的零点个数可能为0、1、2、3、4个.
的零点个数可能为0、1、2、3、4个.
其中正确命题的序号是______.