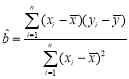题目内容
【题目】已知圆锥的顶点为![]() ,底面圆心为
,底面圆心为![]() ,母线长为
,母线长为![]() ,
,![]() ,
,![]() 、
、![]() 是底面半径,且:
是底面半径,且:![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 的中点,如图所示:
的中点,如图所示:
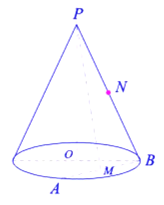
(1)求圆锥的表面积;
(2)求异面直线![]() 和
和![]() 所成的角的大小,并求
所成的角的大小,并求![]() 、
、![]() 两点在圆锥侧面上的最短距离.
两点在圆锥侧面上的最短距离.
【答案】(1)![]() ;(2)
;(2)![]() 、
、![]() 夹角为
夹角为![]() ,最短距离为
,最短距离为![]()
【解析】
(1)由![]() 求得底面圆半径,根据圆锥表面积公式可求得结果;
求得底面圆半径,根据圆锥表面积公式可求得结果;
(2)作![]() ,根据异面直线所成角定义可知所成角为
,根据异面直线所成角定义可知所成角为![]() ;根据向量数量积为零可知
;根据向量数量积为零可知![]() ,进而得到
,进而得到![]() ,根据线面垂直性质知
,根据线面垂直性质知![]() ,得到线面垂直关系
,得到线面垂直关系![]() 平面
平面![]() ,由线面垂直性质得
,由线面垂直性质得![]() ,根据长度关系可求得
,根据长度关系可求得![]() ,进而求得异面直线所成角;求得圆锥侧面展开图圆心角后,根据弧长关系可求得
,进而求得异面直线所成角;求得圆锥侧面展开图圆心角后,根据弧长关系可求得![]() ,由余弦定理可求得结果.
,由余弦定理可求得结果.
(1)由题意得:底面圆半径![]()
![]() 圆锥表面积
圆锥表面积![]()
(2)作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]()
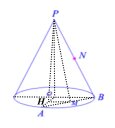
![]() 异面直线
异面直线![]() 与
与![]() 所成角即为
所成角即为![]() 与
与![]() 所成角,即
所成角,即![]()
![]()
![]() ,又
,又![]()
![]()
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]()
![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
又![]() 平面
平面![]()
![]()
![]() 为
为![]() 中点,
中点,![]()
![]() 为
为![]() 中点
中点
![]() ,
,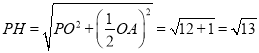
![]()
![]()
即异面直线![]() 与
与![]() 所成角大小为
所成角大小为![]()
由![]() 得:
得:![]() ,即圆锥侧面展开图扇形圆心角为
,即圆锥侧面展开图扇形圆心角为![]()
圆锥侧面展开图如下图所示:
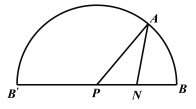
![]()
![]()
![]() 为
为![]() 中点
中点 ![]()
在![]() 中,由余弦定理可得:
中,由余弦定理可得:![]()
![]() ,即
,即![]() 两点在圆锥侧面上的最短距离为
两点在圆锥侧面上的最短距离为![]()

练习册系列答案
相关题目