ЬтФПФкШн
ЁОЬтФПЁПЖЈвхЃКгЩЭждВЕФСНИіНЙЕуКЭЖЬжсЕФвЛИіЖЅЕузщГЩЕФШ§НЧаЮГЦЮЊИУЭждВЕФЁАЬиеїШ§НЧаЮЁБЃЎШчЙћСНИіЭждВЕФЁАЬиеїШ§НЧаЮЁБЪЧЯрЫЦЕФЃЌдђГЦетСНИіЭждВЪЧЁАЯрЫЦЭждВЁБЃЌВЂНЋШ§НЧаЮЕФЯрЫЦБШГЦЮЊЭждВЕФЯрЫЦБШЃЎвбжЊЭждВ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШєЭждВ![]() ЃЌХаЖЯ
ЃЌХаЖЯ![]() гы
гы![]() ЪЧЗёЯрЫЦЃПШчЙћЯрЫЦЃЌЧѓГі
ЪЧЗёЯрЫЦЃПШчЙћЯрЫЦЃЌЧѓГі![]() гы
гы![]() ЕФЯрЫЦБШЃЛШчЙћВЛЯрЫЦЃЌЧыЫЕУїРэгЩЃЛ
ЕФЯрЫЦБШЃЛШчЙћВЛЯрЫЦЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉаДГігыЭждВ![]() ЯрЫЦЧвНЙЕудк
ЯрЫЦЧвНЙЕудк![]() жсЩЯЁЂЖЬАыжсГЄЮЊ
жсЩЯЁЂЖЬАыжсГЄЮЊ![]() ЕФЭждВ
ЕФЭждВ![]() ЕФБъзМЗНГЬЃЛШєдкЭждВ
ЕФБъзМЗНГЬЃЛШєдкЭждВ![]() ЩЯДцдкСНЕу
ЩЯДцдкСНЕу![]() ЁЂ
ЁЂ![]() ЙигкжБЯп
ЙигкжБЯп![]() ЖдГЦЃЌЧѓЪЕЪ§
ЖдГЦЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉШчЭМЃКжБЯп![]() гыСНИіЁАЯрЫЦЭждВЁБ
гыСНИіЁАЯрЫЦЭждВЁБ![]() КЭ
КЭ![]() ЗжБ№НЛгкЕу
ЗжБ№НЛгкЕу![]() КЭЕу
КЭЕу![]() ЃЌЪддкЭждВ
ЃЌЪддкЭждВ![]() КЭЭждВ
КЭЭждВ![]() ЩЯЗжБ№зїГіЕу
ЩЯЗжБ№зїГіЕу![]() КЭЕу
КЭЕу![]() ЃЈЗЧЭждВЖЅЕуЃЉЃЌЪЙ
ЃЈЗЧЭждВЖЅЕуЃЉЃЌЪЙ![]() КЭ
КЭ![]() зщГЩвд
зщГЩвд![]() ЮЊЯрЫЦБШЕФСНИіЯрЫЦШ§НЧаЮЃЌаДГіОпЬхзїЗЈЃЎЃЈВЛБижЄУїЃЉ
ЮЊЯрЫЦБШЕФСНИіЯрЫЦШ§НЧаЮЃЌаДГіОпЬхзїЗЈЃЎЃЈВЛБижЄУїЃЉ
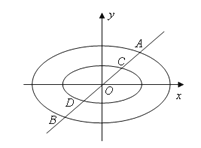
ЁОД№АИЁПЃЈ1ЃЉ ЯрЫЦБШЮЊ![]() ЃЈ2ЃЉ
ЃЈ2ЃЉ![]() ЃЈ3ЃЉЯъМћНтЮі
ЃЈ3ЃЉЯъМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЭждВ![]() гы
гы![]() ЯрЫЦЃЎ
ЯрЫЦЃЎ
вђЮЊЭждВ![]() ЕФЬиеїШ§НЧаЮЪЧбќГЄЮЊ4ЃЌЕзБпГЄЮЊ
ЕФЬиеїШ§НЧаЮЪЧбќГЄЮЊ4ЃЌЕзБпГЄЮЊ![]() ЕФЕШбќШ§НЧаЮЃЌ
ЕФЕШбќШ§НЧаЮЃЌ
ЖјЭждВ![]() ЕФЬиеїШ§НЧаЮЪЧбќГЄЮЊ2ЃЌЕзБпГЄЮЊ
ЕФЬиеїШ§НЧаЮЪЧбќГЄЮЊ2ЃЌЕзБпГЄЮЊ![]() ЕФЕШбќШ§НЧаЮЃЌ
ЕФЕШбќШ§НЧаЮЃЌ
вђДЫСНИіЕШбќШ§НЧаЮЯрЫЦЃЌЧвЯрЫЦБШЮЊ![]()
ЃЈ2ЃЉЭждВ![]() ЕФЗНГЬЮЊЃК
ЕФЗНГЬЮЊЃК![]()
Щш![]() ЃЌЕу
ЃЌЕу![]() ЃЌ
ЃЌ![]() жаЕуЮЊ
жаЕуЮЊ![]() ЃЌ
ЃЌ
дђ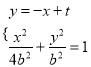 ЃЌЫљвд
ЃЌЫљвд![]()
дђ![]()
вђЮЊжаЕудкжБЯп![]() ЩЯЃЌЫљвдга
ЩЯЃЌЫљвдга![]() ЃЌ
ЃЌ![]()
МДжБЯп![]() ЕФЗНГЬЮЊЃК
ЕФЗНГЬЮЊЃК![]() ЃЌ
ЃЌ
гЩЬтвтПЩжЊЃЌжБЯп![]() гыЭждВ
гыЭждВ![]() гаСНИіВЛЭЌЕФНЛЕуЃЌ
гаСНИіВЛЭЌЕФНЛЕуЃЌ
МДЗНГЬ![]() гаСНИіВЛЭЌЕФЪЕЪ§НтЃЌ
гаСНИіВЛЭЌЕФЪЕЪ§НтЃЌ
Ыљвд![]() ЃЌМД
ЃЌМД![]()
ЃЈ3ЃЉзїЗЈ1ЃКЙ§дЕузїжБЯп![]() ЃЌНЛЭждВ
ЃЌНЛЭждВ![]() КЭЭждВ
КЭЭждВ![]() гкЕу
гкЕу![]() КЭЕу
КЭЕу![]() ЃЌдђ
ЃЌдђ![]() КЭ
КЭ![]() МДЮЊЫљЧѓЯрЫЦШ§НЧаЮЃЌЧвЯрЫЦБШЮЊ
МДЮЊЫљЧѓЯрЫЦШ§НЧаЮЃЌЧвЯрЫЦБШЮЊ![]() ЃЎ
ЃЎ
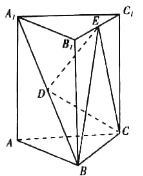
зїЗЈ2ЃКЙ§ЕуAЁЂЕуCЗжБ№зі![]() жсЃЈЛђ
жсЃЈЛђ![]() жсЃЉЕФДЙЯпЃЌНЛЭждВ
жсЃЉЕФДЙЯпЃЌНЛЭждВ![]() КЭЭждВ
КЭЭждВ![]() гкЕу
гкЕу![]() КЭЕу
КЭЕу![]() ЃЌдђ
ЃЌдђ![]() КЭ
КЭ![]() МДЮЊЫљЧѓЯрЫЦШ§НЧаЮЃЌЧвЯрЫЦБШЮЊ
МДЮЊЫљЧѓЯрЫЦШ§НЧаЮЃЌЧвЯрЫЦБШЮЊ![]() ЃЎ
ЃЎ

 жаПМНтЖСПМЕуОЋСЗЯЕСаД№АИ
жаПМНтЖСПМЕуОЋСЗЯЕСаД№АИ