Question

【题目】已知直线y=﹣x+1与椭圆 + =1（a＞b＞0）相交于A、B两点．
①若椭圆的离心率为 ，焦距为2，求线段AB的长；
②若向量 与向量 互相垂直（其中O为坐标原点），当椭圆的离心率e∈[ ， ]时，求椭圆的长轴长的最大值．

Answer 1

【答案】解：①∵ ，2c=2，

∴a= ，b= ，

∴椭圆的方程为 ．

联立 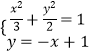，消去y得：5x2﹣6x﹣3=0，

设A（x1，y1），B（x2，y2），则 ， ，

∴|AB|=

=

= ．

②设A（x1，y1），B（x2，y2），

∵ ，∴ ，

即x1x2+y1y2=0，

由 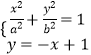，消去y得（a2+b2）x2﹣2a2x+a2（1﹣b2）=0，

由△=（﹣2a2）2﹣4a2（a2+b2）（1﹣b2）＞0，整理得a2+b2＞1

∵ ， ，

∴y1y2=（﹣x1+1）（﹣x2+1）=x1x2﹣（x1+x2）+1，

∴x1x2+y1y2=0，得：2x1x2﹣（x1+x2）+1=0，

∴ ，

整理得：a2+b2﹣2a2b2=0．

∴b2=a2﹣c2=a2﹣a2e2，代入上式得

2a2=1+ ，∴ ，

∵ ，

∴ ，∴ ，

∴ ，∴ ，

∴ 适合条件a2+b2＞1．

由此得 ，∴ ，

故长轴长的最大值为 ．

【解析】①先由已知条件可得椭圆的标准方程，再利用弦长公式可得线段AB的长；②设A，B的坐标，由 ⊥可得 x1x2+y1y2=0，联立方程组消去y得（a2+b2）x2﹣2a2x+a2（1﹣b2）=0，再由可得a2+b2＞1，进而由韦达定理可得a2+b2﹣2a2b2=0，由此可得长轴长的最大值．