题目内容
1．一个立方体骰子的六个面分别标有数字1，2，2，3，3，4；另一个立方体骰子的六个面分别标有数字1，3，4，5，6，8．掷两粒骰子，则其最上面所标的两数之和为7的概率是$\frac{1}{6}$．分析 扔2颗骰子的所有情况共有36种情况，得出满足条件的结果，得出概率即可
解答 解：在36对可能的结果中，和为7的有6对：（1，6），（2，5），（2，5），（3，4），（3，4），（4，3）．
∴得到两数之和为7的概率是$\frac{6}{36}=\frac{1}{6}$．
故答案为：$\frac{1}{6}$
点评 本题主要考查了古典概型的概念和在实际中的应用，属于基础题型．
练习册系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
12．已知函数f（x）=2ax3-3x2+1，若 f（x）存在唯一的零点x0，且x0＞0，则a的取值范围是（ ）
| A． | （1，+∞） | B． | （0，1） | C． | （-1，0） | D． | （-∞，-1） |
9．直线2x-5y+20=0与坐标轴交于两点，以坐标轴为对称轴，以其中一个点为焦点且另一个点为虚轴端点的双曲线的标准方程是（ ）
| A． | $\frac{{x}^{2}}{84}$-$\frac{{y}^{2}}{16}$=1 | B． | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{84}$=1 | ||
| C． | $\frac{{x}^{2}}{100}$-$\frac{{y}^{2}}{84}$=1 | D． | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{84}$=1或$\frac{{x}^{2}}{100}$-$\frac{{y}^{2}}{84}$=1 |
16．非零向量$\overrightarrow{a}$，$\overrightarrow{b}$，若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|，则（ ）
| A． | $\overrightarrow{a}$与$\overrightarrow{b}$方向相同 | B． | $\overrightarrow{a}$与$\overrightarrow{b}$方向相反 | C． | $\overrightarrow{a}$与$\overrightarrow{b}$垂直 | D． | 以上都不对 |
6．执行如图所示的程序框图，输出结果S=（ ）
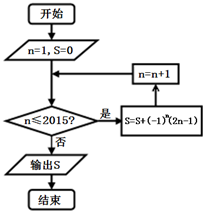
| A． | 2015 | B． | 2016 | C． | -2015 | D． | -2016 |
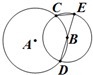如图，圆A与圆B交于C、D两点，圆心B在圆A上，DE为圆B的直径．已知CE=1，DE=4，则圆A的半径为4．