题目内容
2.已知各项均为正数的等比数列{an}中,3a1,$\frac{1}{2}$a3,2a2,成等差数列,则$\frac{{a}_{2014}+{a}_{2015}}{{a}_{2011}+{a}_{2012}}$=( )| A. | -1或3 | B. | 3 | C. | 27 | D. | -1或27 |
分析 先根据等差数列的性质建立等式求得公比q,进而代入原式求得答案.
解答 解:依题意可知a3=3a1+2a2,
∴a1q2=3a1+2a1q,整理求得q=3或-1(舍去),
∴$\frac{{a}_{2014}+{a}_{2015}}{{a}_{2011}+{a}_{2012}}$=$\frac{{a}_{2014}+{a}_{2014}q}{\frac{{a}_{2014}}{{q}^{3}}+\frac{{a}_{2014}}{{q}^{2}}}$=$\frac{1+q}{\frac{1}{{q}^{3}}+\frac{1}{{q}^{2}}}$=q3=27,
故选:C.
点评 本题主要考查了等比数列和等差数列性质的运用.等差中项是解决等差数列问题的常用性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知函数f(x)=2ax3-3x2+1,若 f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( )
| A. | (1,+∞) | B. | (0,1) | C. | (-1,0) | D. | (-∞,-1) |
17.过椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的右焦点F作两条相互垂直的直线分别交椭圆于A,B,C,D四点,则$\frac{1}{|AB|}+\frac{1}{|CD|}$的值为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | 1 | D. | $\frac{7}{12}$ |
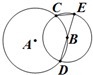 如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径.已知CE=1,DE=4,则圆A的半径为4.
如图,圆A与圆B交于C、D两点,圆心B在圆A上,DE为圆B的直径.已知CE=1,DE=4,则圆A的半径为4.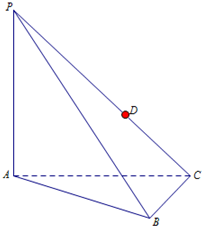 如图,在三棱锥P-ABC中,△ABC为等边三角形,AB=2,AP⊥平面ABC,D为PC上的动点.
如图,在三棱锥P-ABC中,△ABC为等边三角形,AB=2,AP⊥平面ABC,D为PC上的动点.