题目内容
19.已知直线m,n和平面α,则m∥n的必要不充分条件是( )| A. | 直线m,n和平面α成等角 | B. | m⊥α且n⊥α | ||
| C. | m∥α且n?α | D. | m∥α且n∥α |
分析 A.利用线面角的定义可知:直线m,n和平面α,m∥n⇒直线m,n和平面α成等角,反之不成立,即可判断出关系;
B.利用线面垂直的性质定理即可判断出正误;
C.由m∥α且n?α⇒m∥n或异面直线,即可判断出关系;
D.m∥α且n∥α,则m∥n、相交或异面直线,即可判断出关系.
解答 解:A.直线m,n和平面α,m∥n⇒直线m,n和平面α成等角,反之不成立,因此直线m,n和平面α,则m∥n的必要不充分条件是直线m,n和平面α成等角,正确;
B.m⊥α且n⊥α⇒m∥n,反之不成立,因此m⊥α且n⊥α是m∥n的充分不必要条件;
C.m∥α且n?α⇒m∥n或异面直线,因此m∥α且n?α是m∥n的既不必要也不充分条件;
D.m∥α且n∥α,则m∥n、相交或异面直线,m∥α且n∥α是m∥n的既不必要也不充分条件.
故选:A.
点评 本题考查了空间中线面位置关系,考查了推理能力,属于中档题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
9.直线2x-5y+20=0与坐标轴交于两点,以坐标轴为对称轴,以其中一个点为焦点且另一个点为虚轴端点的双曲线的标准方程是( )
| A. | $\frac{{x}^{2}}{84}$-$\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{84}$=1 | ||
| C. | $\frac{{x}^{2}}{100}$-$\frac{{y}^{2}}{84}$=1 | D. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{84}$=1或$\frac{{x}^{2}}{100}$-$\frac{{y}^{2}}{84}$=1 |
4.已知双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点与抛物线C2:x=$\frac{1}{8}$y2的焦点重合,直线l为bx-ay+8=0,P为C2上一个动点,P到直线l的距离为d1,到C2准线的距离为d2,当d1+d2的最小值为5时,C1的方程为( )
| A. | y2-$\frac{{x}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{3}$-y2=1 | D. | x2-$\frac{{y}^{2}}{3}$=1 |
8.运行如图的程序框图,若输入n=2015,则输出的a=( )
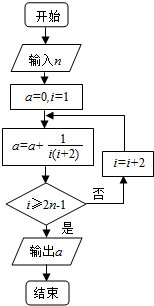

| A. | $\frac{2015}{4031}$ | B. | $\frac{4030}{4031}$ | C. | $\frac{2014}{4029}$ | D. | $\frac{2015}{4029}$ |
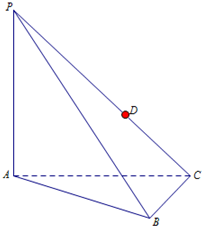 如图,在三棱锥P-ABC中,△ABC为等边三角形,AB=2,AP⊥平面ABC,D为PC上的动点.
如图,在三棱锥P-ABC中,△ABC为等边三角形,AB=2,AP⊥平面ABC,D为PC上的动点.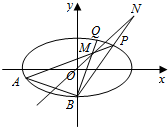 如图,已知椭圆C:$\frac{x^2}{2}$+y2=1,点B坐标为(0,-1),过点B的直线交椭圆C于y轴左侧另外一点A,且线段AB的中点E在直线y=x上.
如图,已知椭圆C:$\frac{x^2}{2}$+y2=1,点B坐标为(0,-1),过点B的直线交椭圆C于y轴左侧另外一点A,且线段AB的中点E在直线y=x上.