题目内容
8. 如图,在多面体ABCDEF中,正方形ADEF与梯形ABCD所在平面互相垂直,已知AB∥CD,AD⊥CD,AB=AD=1,CD=2.
如图,在多面体ABCDEF中,正方形ADEF与梯形ABCD所在平面互相垂直,已知AB∥CD,AD⊥CD,AB=AD=1,CD=2.(Ⅰ)求证:BC⊥平面BDE;
(Ⅱ)求点C到平面BDF的距离.
分析 (Ⅰ)根据直线与平面垂直的判定定理可知只需证BC与平面BDE内两相交直线垂直,根据面面垂直的性质可知ED⊥平面ABCD,则ED⊥BC,根据勾股定理可知BC⊥BD,满足定理所需条件;
(Ⅱ)由等体积可得点C到平面BDF的距离.
解答 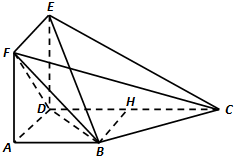 (Ⅰ)证明:在梯形ABCD中,取CD中点H,连接BH,
(Ⅰ)证明:在梯形ABCD中,取CD中点H,连接BH,
因为AB∥CD,AD⊥CD,AB=AD,所以四边形ADHB为正方形,
又AD2A+AB2=BD2=2,HC2+HB2=BC2,所以BD2+BC2=CD2,
所以BC⊥BD …(3分)
又平面ADEF⊥平面ABCD,平面ADEF∩平面ABCD=AD,DE⊥AD,
所以DE⊥平面ABCD,…(5分)
所以BC⊥DE,
又BD∩DE=D,
故BC⊥平面BDE.…(6分)
(Ⅱ)解:设点C到平面BDF的距离为h,
由(Ⅰ)知FD=BD=FB=$\sqrt{2}$,所以△BDF为等边三角形,
其面积S△BDF=$\frac{\sqrt{3}}{4}×(\sqrt{2})^{2}$=$\frac{\sqrt{3}}{2}$,又△CDB的面积S△CDB=$\frac{1}{2}BH•CD$=1 …(8分)
所以由等体积可得$\frac{1}{3}×1×1=\frac{1}{3}×\frac{\sqrt{3}}{2}h$,
因此h=$\frac{2\sqrt{3}}{3}$,即点C到平面BDF的距离为$\frac{2\sqrt{3}}{3}$.…(12分)
点评 本题考查的知识点是直线与平面垂直的判定,考查点C到平面BDF的距离,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
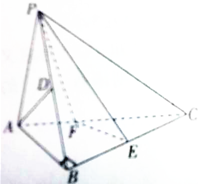 如图在三棱锥P-ABC中,已知AB⊥BC,PA⊥BC,PA=AB=BC=PB,点D,E分别为PB,BC的中点.
如图在三棱锥P-ABC中,已知AB⊥BC,PA⊥BC,PA=AB=BC=PB,点D,E分别为PB,BC的中点.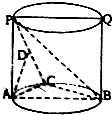 已知圆柱轴截面为PQBA,C为底面圆周上异于A、B的一点,D为PC中点.
已知圆柱轴截面为PQBA,C为底面圆周上异于A、B的一点,D为PC中点.
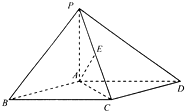 如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥底面ABCD,∠PCD=90°,PA=AB=AC=2
如图,四棱锥P-ABCD的底面ABCD是平行四边形,PA⊥底面ABCD,∠PCD=90°,PA=AB=AC=2