题目内容
18.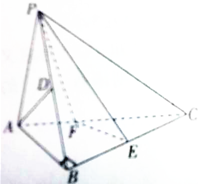 如图在三棱锥P-ABC中,已知AB⊥BC,PA⊥BC,PA=AB=BC=PB,点D,E分别为PB,BC的中点.
如图在三棱锥P-ABC中,已知AB⊥BC,PA⊥BC,PA=AB=BC=PB,点D,E分别为PB,BC的中点.(1)求异面直线AD与PE所成的角;
(2)若F在线段AC上,且$\frac{AF}{FC}$=$\frac{1}{2}$,求证AD∥平面PEF;
(3)求二面角P-AC-B的.
分析 (1)AB⊥BC,PA⊥BC,PA∩AB=A,可得BC⊥平面PAB,平面ABC⊥平面PAB.取AB的中点O,连接PO,可得PO⊥AB,PO⊥平面ABC.取AC的中点M,连接OM,利用三角形中位线定理及其线面垂直的性质可得:OM⊥AB,OM⊥OP.不妨取AB=2,则PA=AB=BC=PB=2,计算出$\overrightarrow{AD}•\overrightarrow{EP}$即可得出.
(2)由F在线段AC上,且$\frac{AF}{FC}$=$\frac{1}{2}$,可得$\overrightarrow{OF}=\frac{1}{3}\overrightarrow{OC}+\frac{2}{3}\overrightarrow{OA}$.设平面PEF的法向量为$\overrightarrow{m}$=(x1,y1,z1),利用$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PE}=0}\\{\overrightarrow{n}•\overrightarrow{PF}=0}\end{array}\right.$,可得$\overrightarrow{m}$,只要证明$\overrightarrow{m}•\overrightarrow{AD}$=0即可.
(3)设平面PAC的法向量为:$\overrightarrow{n}$=(x2,y2,z2),利用$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PF}=0}\\{\overrightarrow{n}•\overrightarrow{AC}=0}\end{array}\right.$,可得$\overrightarrow{n}$,取平面ABC的法向量为$\overrightarrow{v}$=(0,0,1),利用$cos<\overrightarrow{n},\overrightarrow{v}>$=$\frac{\overrightarrow{n}•\overrightarrow{v}}{|\overrightarrow{n}||\overrightarrow{v}|}$即可得出.
解答 (1)解:∵AB⊥BC,PA⊥BC,PA∩AB=A,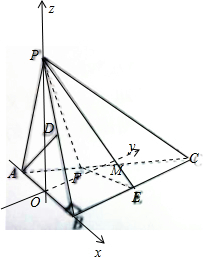
∴BC⊥平面PAB,又BC?平面BC,∴平面ABC⊥平面PAB.
平面ABC∩平面PAB=AB.
取AB的中点O,连接PO,则PO⊥AB,∴PO⊥平面ABC,
取AC的中点M,连接OM,则$OM\underset{∥}{=}\frac{1}{2}BC$,
∴OM⊥AB,OM⊥OP.
不妨取AB=2,则PA=AB=BC=PB=2,
又点D,E分别为PB,BC的中点.
∴A(-1,0,0),O(0,0,0),B(1,0,0),P$(0,0,\sqrt{3})$,C(1,2,0),D$(\frac{1}{2},0,\frac{\sqrt{3}}{2})$,E(1,1,0).
∴$\overrightarrow{AD}$=$(\frac{3}{2},0,\frac{\sqrt{3}}{2})$,$\overrightarrow{EP}$=$(-1,-1,\sqrt{3})$,
∴$\overrightarrow{AD}•\overrightarrow{EP}$=$-\frac{3}{2}+\frac{\sqrt{3}}{2}×\sqrt{3}$=0.
∴异面直线AD与PE所成的角为90°.
(2)证明:∵F在线段AC上,且$\frac{AF}{FC}$=$\frac{1}{2}$,∴$\overrightarrow{OF}=\frac{1}{3}\overrightarrow{OC}+\frac{2}{3}\overrightarrow{OA}$=$(-\frac{1}{3},\frac{2}{3},0)$.
设平面PEF的法向量为$\overrightarrow{m}$=(x1,y1,z1),
$\overrightarrow{PE}$=$(1,1,-\sqrt{3})$,$\overrightarrow{PF}$=$(-\frac{1}{3},\frac{2}{3},-\sqrt{3})$.
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PE}=0}\\{\overrightarrow{n}•\overrightarrow{PF}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{{x}_{1}+{y}_{1}-\sqrt{3}{z}_{1}=0}\\{-\frac{1}{3}{x}_{1}+\frac{2}{3}{y}_{1}-\sqrt{3}{z}_{1}=0}\end{array}\right.$,可取$\overrightarrow{m}$=$(-1,4,\sqrt{3})$.
∴$\overrightarrow{m}•\overrightarrow{AD}$=$-\frac{3}{2}+0+\frac{\sqrt{3}}{2}×\sqrt{3}$=0,
又A∉平面PEF,
∴AD∥平面PEF;
(3)解:$\overrightarrow{AC}$=(2,2,0),
设平面PAC的法向量为:$\overrightarrow{n}$=(x2,y2,z2),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PF}=0}\\{\overrightarrow{n}•\overrightarrow{AC}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{-\frac{1}{3}{x}_{2}+\frac{2}{3}{y}_{2}-\sqrt{3}{z}_{2}=0}\\{2{x}_{2}+2{y}_{2}=0}\end{array}\right.$,可取$\overrightarrow{n}$=$(-1,1,\frac{\sqrt{3}}{9})$,
取平面ABC的法向量为$\overrightarrow{v}$=(0,0,1).
∴$cos<\overrightarrow{n},\overrightarrow{v}>$=$\frac{\overrightarrow{n}•\overrightarrow{v}}{|\overrightarrow{n}||\overrightarrow{v}|}$=$\frac{\frac{\sqrt{3}}{9}}{1×\sqrt{2+\frac{1}{27}}}$=$\frac{\sqrt{55}}{55}$.
∴二面角P-AC-B的余弦值为$\frac{\sqrt{55}}{55}$.
点评 本题考查了通过建立空间直角坐标系利用法向量求空间距离与空间角、向量垂直与数量积的关系、线面平行与垂直,考查了推理能力与计算能力,属于中档题.

| A. | 15 | B. | 200 | C. | 240 | D. | 2160 |
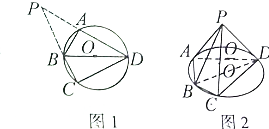 如图1,以BD为直径的圆O经过A,C两点,延长DA,CB交于P点,将PAB沿线段AB折起,使P点在底面ABCD的射影恰为AD的中点Q,如图2,AB=BC=1,BD=2,线段PB,PC的中点为E、F.
如图1,以BD为直径的圆O经过A,C两点,延长DA,CB交于P点,将PAB沿线段AB折起,使P点在底面ABCD的射影恰为AD的中点Q,如图2,AB=BC=1,BD=2,线段PB,PC的中点为E、F.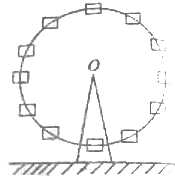 如图,游乐场中的摩天轮匀速旋转,每转一圈需要12分钟,其中圆心O距离地面40.5米,半径40米,如果你从最低处登上摩天轮,那么你与地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时,请解答下列问题.
如图,游乐场中的摩天轮匀速旋转,每转一圈需要12分钟,其中圆心O距离地面40.5米,半径40米,如果你从最低处登上摩天轮,那么你与地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时,请解答下列问题. 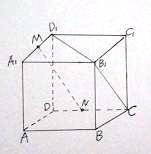 正方体中,M、N分别是A1D1、DC的中点,
正方体中,M、N分别是A1D1、DC的中点, 如图,在多面体ABCDEF中,正方形ADEF与梯形ABCD所在平面互相垂直,已知AB∥CD,AD⊥CD,AB=AD=1,CD=2.
如图,在多面体ABCDEF中,正方形ADEF与梯形ABCD所在平面互相垂直,已知AB∥CD,AD⊥CD,AB=AD=1,CD=2.