题目内容

5．函数f（x）=2x3-3x2-12x+5在[0，3]上的最值．

分析 求出函数的导数，求得导数为0的解，注意函数的定义域，求得极值和端点处的函数值，即可得到最值．

解答 解：函数f（x）=2x3-3x2-12x+5的导数
f′（x）=6x2-6x-12，
令f′（x）=0，即6x2-6x-12=0，
则x=-1或x=2．
又x∈[0，3]，故x=-1应舍去．
当x变化时，f′（x）与f（x）的变化情况如表：

x0（0，2）2（2，3）3
f′（x）-0+
f（x）5↘-15↗-4
∴f（x）在[0，3]上的最大值为5，最小值为-15．

点评 本题考查导数的运用：求最值，主要考查求函数的最值的方法，注意函数的定义域的运用，属于基础题．

练习册系列答案
相关题目
10．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），直线l1：$\frac{x}{a}$-$\frac{y}{b}$=1被椭圆C截得的弦长为2$\sqrt{2}$，且e=$\frac{\sqrt{6}}{3}$，过椭圆C的右焦点且斜率为$\sqrt{3}$的直线l2被椭圆C截得弦长AB，
（1）求椭圆的方程；
（2）弦AB的长度．
11．为备战2016年奥运会，甲、乙两位射击选手进行了强化训练，现分别从他们的强化训练期间的若干次平均成绩中随机抽取8次，记录如下：
甲：8.3，9.0，7.9，7.8，9.4，8.9，8.4，8.3；
乙：9.2，9.5，8.0，7.5，8.2，8.1，9.0，8.5．
（1）现要从中选派一人参见奥运会封闭集训，从统计学角度，你认为派哪位选手参加合理？简单说明理由；
（2）若将频率视为概率，对选手乙在今后的三次比赛成绩进行预测，记这三次成绩中不低于8.5分的次数为ξ，求ξ的分布列及均值E（ξ）．
8．如图，在多面体ABCDEF中，正方形ADEF与梯形ABCD所在平面互相垂直，已知AB∥CD，AD⊥CD，AB=AD=1，CD=2．
（Ⅰ）求证：BC⊥平面BDE；
（Ⅱ）求点C到平面BDF的距离．
15．若cos（2α+$\frac{π}{6}$）=$\frac{4}{5}$，则sin（α+$\frac{π}{12}$）=$±\frac{\sqrt{10}}{10}$．
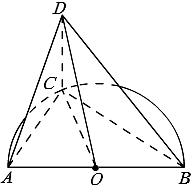10．如图，已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点，AB是直径，CD=1，直线CD⊥平面ABC．
（1）证明：AC⊥BD；
（2）在DB上是否存在一点M，使得OM∥平面DAC，若存在，请确定点M的位置，并证明之；若不存在，请说明理由；
（3）求点C到平面ABD的距离．
17．已知函数f（x）=$\frac{lnx+a}{x}$（a∈R），f′（1）=0．
（1）求实数a的值；
（2）证明当x≥1时，f（x）≤1．
14．已知函数 f（x）=ax3+bx2+cx在R上是奇函数，且 f（-1）=-2，f（2）=10．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）说明 f（x）在R上的单调性（不需要证明）；
（Ⅲ）若关于x的不等式 f（x2-9）+f（kx+3k）＜0在 x∈（0，1）上恒成立，求实数k是的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网