题目内容
8.四面体ABCD中,点G1,G2,G3,G4分别是△BCD,△ACD,△ABD,△ABC的重心.求证:AG1,BG2,CG3,DG4交于一点.分析 由三角形重心的性质说明AG1,BG2相交于一点M,然后证明CG3,DG4过点M即可.
解答  证明:如图,
证明:如图,
∵G1,G2分别是△BCD,△ACD的重心,
连接BG2,AG1并延长,交CD于点E,在平面ABE中,设AG1∩BG2=M,则$\frac{{G}_{1}M}{MA}=\frac{{G}_{2}M}{MB}=\frac{1}{3}$,
连接DG1,AG4并延长交于N,在平面ADN中,设AG1∩DG4=M′,则$\frac{{G}_{1}M′}{M′A}=\frac{{G}_{4}M′}{M′D}=\frac{1}{3}$,
从而可得M,M′重合,即AG1,BG2,DG4交于一点M,
同理可得CG3过点M.
即AG1,BG2,CG3,DG4交于一点.
点评 本题考查了棱锥的结构特征,考查了三角形重心的性质,训练了统一法证明线共点问题,是中档题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
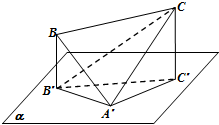 如图,已知边长为2的正△A′BC,顶点A′在平面α内,顶点B,C在平面α外的同一侧,点B′,C′分别为B,C在平面α上的投影,设|BB′|≤|CC′|,直线CB′与平面A′CC′所成的角为φ.若△A′B′C′是以∠A′为直角的直角三角形,则tanφ的范围为$[{\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}})$.
如图,已知边长为2的正△A′BC,顶点A′在平面α内,顶点B,C在平面α外的同一侧,点B′,C′分别为B,C在平面α上的投影,设|BB′|≤|CC′|,直线CB′与平面A′CC′所成的角为φ.若△A′B′C′是以∠A′为直角的直角三角形,则tanφ的范围为$[{\frac{{\sqrt{2}}}{2},\frac{{\sqrt{3}}}{2}})$. 如图,在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.
如图,在正三棱柱ABC-A1B1C1中,点D在边BC上,AD⊥C1D.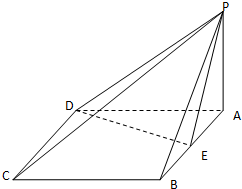 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点. 如图,在长方体ABCD-A1B1C1D1中,A1A=$\sqrt{2}$,AD=1,DC=2,点E为AB中点.
如图,在长方体ABCD-A1B1C1D1中,A1A=$\sqrt{2}$,AD=1,DC=2,点E为AB中点.