题目内容
3.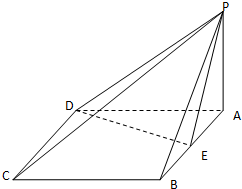 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点.(Ⅰ)求证:面PDE⊥面PAB;
(Ⅱ)若PA=AB=2,求PC与面PAD所成角的正弦值.
分析 (Ⅰ)根据几何性质得出DE⊥AB,DE⊥AP,运用定理得出DE⊥面PAB,借助面面垂直的判定即可得证.
(II)得证CF⊥面PAD,判断出∠CPF为PA与面PAD所成角,运用三角形Rt△CAP求解即可.
解答  (Ⅰ)证明∵底面ABCD是菱形,∠BCD=60°,
(Ⅰ)证明∵底面ABCD是菱形,∠BCD=60°,
∴△ABD为正三角形,
E是AB的中点,DE⊥AB,
PA⊥面ABCD,DE?面ABCD,
∴DE⊥AP,
∴DE⊥面PAB,
∵DE?面PDE,
∴面PED⊥面PAB,
(II)在面ABCD内,过点C作CF⊥AD,交AD延长线于F,连接PF,
∵PA⊥面ABCD,CF?面ABCD,
∴PA⊥CF,
又CF⊥面PAD,
∴∠CPF为PA与面PAD所成角,
在Rt△CFD中,∠CDF=60°,
∴CF=$\sqrt{3}$,
在Rt△CAP中AC=2$\sqrt{3}$,PA=2,
∴PC=4,
∴sin∠CPF=$\frac{\sqrt{3}}{4}$.
点评 本题考查了直线平面的垂直问题,直线与平面所成的角的求解,关键是确定垂线,找出平面角,转化到三角形求解.

练习册系列答案
相关题目
11.P是直角△ABC所在平面外一点,若PA⊥平面ABC,PA=AB=AC,则平面PBC和平面ABC夹角的正切值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 2$\sqrt{2}$ |
13.某工厂生产的甲、乙、丙三种型号产品的数量之比为2:3:5,现用分层抽样的方法抽取一个容量为n的样本,其中甲种产品有20件,则n=( )
| A. | 50 | B. | 100 | C. | 150 | D. | 200 |
 如图,在棱长都相等的四面体ABCD中,点E是棱AD的中点.
如图,在棱长都相等的四面体ABCD中,点E是棱AD的中点. 在三棱锥P-ABC中,AC=BC=AP=BP=$\sqrt{2}$,PC=$\sqrt{3}$,AB=2.
在三棱锥P-ABC中,AC=BC=AP=BP=$\sqrt{2}$,PC=$\sqrt{3}$,AB=2. 已知在四棱锥P-ABCD中,底面ABCD是等腰梯形,AD∥BC,∠BAD=60°,PA⊥平面ABCD,AD=2,BC=1,PA=2$\sqrt{2}$,H,G分别为AD,PC的中点.
已知在四棱锥P-ABCD中,底面ABCD是等腰梯形,AD∥BC,∠BAD=60°,PA⊥平面ABCD,AD=2,BC=1,PA=2$\sqrt{2}$,H,G分别为AD,PC的中点. 如图,四棱锥P-ABCD的底面是正方形,侧棱PD⊥底面ABCD,点E是棱PB的中点.
如图,四棱锥P-ABCD的底面是正方形,侧棱PD⊥底面ABCD,点E是棱PB的中点. 从某中学1000名学生中随机抽取m名学生进行问卷调查.根据问卷取得了这m名学生星期日运动锻炼时间(单位:分钟)的数据频率分布直方图,如图,已知抽取的学生中星期日运动时间少于60分钟的人数为5人
从某中学1000名学生中随机抽取m名学生进行问卷调查.根据问卷取得了这m名学生星期日运动锻炼时间(单位:分钟)的数据频率分布直方图,如图,已知抽取的学生中星期日运动时间少于60分钟的人数为5人