题目内容
20.正四棱锥P-ABCD的底边及侧棱长都是2,M,N分别为底边CD,CB上的动点,且CM=CN,当四面体P-AMN的体积最大时,直线PA与面PMN的所成角的大小是45°.分析 由题意画出图形,设CM=CN=x,把四面体P-AMN的底面的面积的平方用含有x的代数式表示,求导得到使底面积最大的x值,再由高一定可得体积最大,由此求出体积最大时直线PA与面PMN的所成角的大小.
解答 解:如图,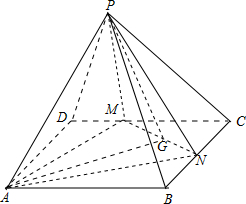
设CM=CN=x,则DM=1-x,MN=$\sqrt{2}x$,
AM2=4+(2-x)2=8-4x+x2,$A{G}^{2}=A{M}^{2}-M{G}^{2}=8-4x+{x}^{2}-\frac{1}{2}{x}^{2}$=$\frac{1}{2}{x}^{2}-4x+8$.
${{S}_{△AMN}}^{2}=\frac{1}{4}(\sqrt{2}x)^{2}•(\frac{1}{2}{x}^{2}-4x+8)$=$\frac{1}{4}{x}^{4}-2{x}^{3}+4{x}^{2}$.
令f(x)=$\frac{1}{4}{x}^{4}-2{x}^{3}+4{x}^{2}$,则f′(x)=x3-6x2+8x,
由f′(x)=0,得x=2或x=4(舍),
∴当x=2时,${{S}_{△AMN}}^{2}$有最大值,即S△AMN有最大值,四面体P-AMN的体积最大.
此时M与D重合,N与B重合,由△BAD≌△DPB,可得直线PA与面PMN的所成角的大小是45°.
故答案为:45°.
点评 本题考查了空间角的求法,考查了利用导数求函数的最值,考查学生灵活处理问题的能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.P是直角△ABC所在平面外一点,若PA⊥平面ABC,PA=AB=AC,则平面PBC和平面ABC夹角的正切值是( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 2$\sqrt{2}$ |
 如图,四棱锥P-ABCD的底面是正方形,侧棱PD⊥底面ABCD,点E是棱PB的中点.
如图,四棱锥P-ABCD的底面是正方形,侧棱PD⊥底面ABCD,点E是棱PB的中点. 从某中学1000名学生中随机抽取m名学生进行问卷调查.根据问卷取得了这m名学生星期日运动锻炼时间(单位:分钟)的数据频率分布直方图,如图,已知抽取的学生中星期日运动时间少于60分钟的人数为5人
从某中学1000名学生中随机抽取m名学生进行问卷调查.根据问卷取得了这m名学生星期日运动锻炼时间(单位:分钟)的数据频率分布直方图,如图,已知抽取的学生中星期日运动时间少于60分钟的人数为5人