题目内容
甲，乙两人进行乒兵球比赛，在每一局比赛中，甲获胜的概率为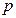
。
(1)如果甲，乙两人共比赛4局，甲恰好负2局的概率不大于其恰好胜3局的概率，试求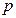的取值范围；
(2)若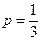
，当采用3局2胜制的比赛规则时，求甲获胜的概率；
(3)如果甲，乙两人比赛6局，那么甲恰好胜3局的概率可能是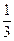
吗？
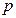。(1)如果甲，乙两人共比赛4局，甲恰好负2局的概率不大于其恰好胜3局的概率，试求
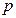的取值范围；(2)若
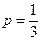，当采用3局2胜制的比赛规则时，求甲获胜的概率；(3)如果甲，乙两人比赛6局，那么甲恰好胜3局的概率可能是
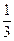吗？⑴
或
⑵
⑶甲恰好胜3局的概率不可能是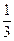
或⑵⑶甲恰好胜3局的概率不可能是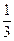设每一局比赛甲获胜的概率为事件A，则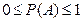
(1)由题意知
即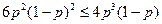
解得或
(2)甲获胜，则有比赛2局，甲全胜，或比赛3局，前2局甲胜1局，第3局甲胜，故
(3)设“比赛6局，甲恰好胜3局”为事件C 则P(C)＝
当P＝0或P＝1时，显然有
又当0＜P＜1时，
故甲恰好胜3局的概率不可能是.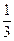
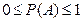
(1)由题意知
即
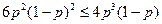解得或(2)甲获胜，则有比赛2局，甲全胜，或比赛3局，前2局甲胜1局，第3局甲胜，故
(3)设“比赛6局，甲恰好胜3局”为事件C 则P(C)＝
当P＝0或P＝1时，显然有
又当0＜P＜1时，
故甲恰好胜3局的概率不可能是
.
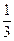练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
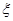的分布列和数学期望；
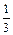，为1的概率为
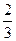.例如若A=10001,其中A1= A5=1，A2= A3= A4=0.记m= A1+A2+ A3+ A4+ A5,求启动仪器一次时，
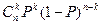，它与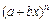
的展开式中第 项系数及其类似，此时a= ,b= ,x= .