题目内容
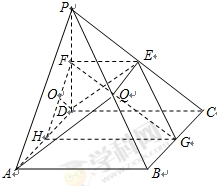
如图,在四棱锥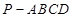 中,
中, 是正方形,
是正方形,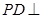 平面
平面 ,
,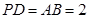 ,
,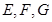 分别是
分别是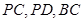 的中点.
的中点.
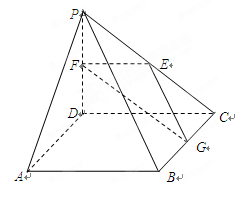
(1)在线段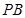 上确定一点
上确定一点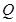 ,使
,使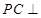 平面
平面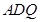 ,并给出证明;
,并给出证明;
(2)证明平面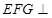 平面
平面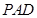 ,并求出
,并求出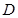 到平面
到平面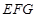 的距离.
的距离.
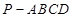 中,
中, 是正方形,
是正方形,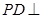 平面
平面 ,
,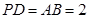 ,
,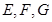 分别是
分别是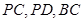 的中点.
的中点.
(1)在线段
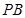 上确定一点
上确定一点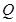 ,使
,使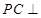 平面
平面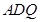 ,并给出证明;
,并给出证明;(2)证明平面
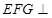 平面
平面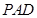 ,并求出
,并求出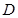 到平面
到平面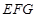 的距离.
的距离.(1)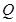 为线段
为线段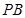 中点时,
中点时,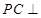 平面
平面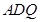 ;(2)
;(2)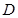 到
到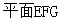 的距离为
的距离为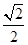 .
.
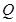 为线段
为线段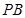 中点时,
中点时,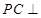 平面
平面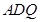 ;(2)
;(2)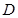 到
到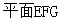 的距离为
的距离为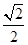 .
.试题分析:
(1)
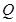 为线段
为线段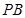 中点,连接
中点,连接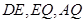 ,可得出
,可得出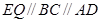 ,所以
,所以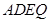 为平面四边形,先证
为平面四边形,先证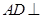 平面
平面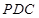 ,所以
,所以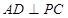 ,又三角形
,又三角形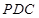 为等腰直角三角形,
为等腰直角三角形,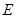 为斜边中点,所以
为斜边中点,所以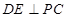 .即可得结论
.即可得结论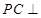 平面
平面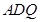 ;
;(2)根据线线垂直
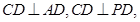 可得线面垂直
可得线面垂直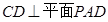 ,
,进而推出面面垂直
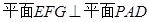 .
.取所以
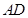 中点所以
中点所以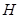 ,证明
,证明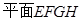 即为
即为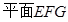 ,因为
,因为 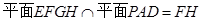 ,在平面
,在平面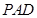 内,作
内,作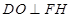 ,垂足为
,垂足为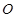 ,则
,则 ,
, 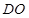 即为
即为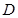 到
到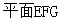 的距离,在三角形
的距离,在三角形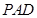 中,
中,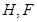 为
为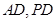 中点,
中点,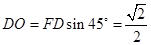 ,即
,即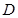 到
到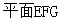 的距离为
的距离为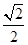 (12分)
(12分)试题解析:(1)
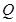 为线段
为线段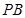 中点时,
中点时,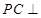 平面
平面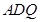 .
. 取
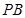 中点
中点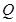 ,连接
,连接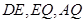 ,
,由于
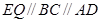 ,所以
,所以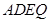 为平面四边形,
为平面四边形,由
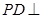 平面
平面 ,得
,得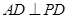 ,
,又
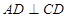 ,
,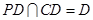 ,所以
,所以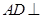 平面
平面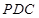 ,
,所以
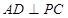 ,
,又三角形
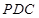 为等腰直角三角形,
为等腰直角三角形,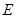 为斜边中点,所以
为斜边中点,所以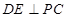 ,
,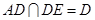 ,所以
,所以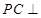 平面
平面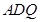 . (5分)
. (5分)(2)因为
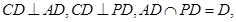 所以
所以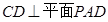 .
.又
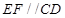 ,所以
,所以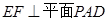 ,所以
,所以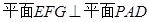 .
.取所以
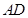 中点所以
中点所以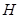 ,连接所以
,连接所以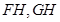 ,则
,则 ,
,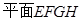 即为
即为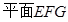 ,
,在平面
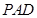 内,作
内,作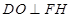 ,垂足为
,垂足为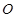 ,则
,则 ,
,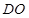 即为
即为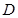 到
到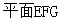 的距离,
的距离,在三角形
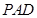 中,
中,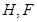 为
为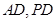 中点,
中点,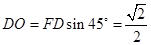 ,
,即
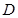 到
到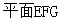 的距离为
的距离为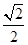 (12分)
(12分) 线面垂直
线面垂直 面面垂直的等价转化方法;
面面垂直的等价转化方法;点到平面的距离,可先做垂线,在解三角形.

练习册系列答案
相关题目
 平面
平面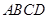 ,
, ,点
,点 是
是 的中点,点
的中点,点 是边
是边 上的动点.
上的动点.
 的体积;
的体积; 与平面
与平面 的位置关系,并说明理由;
的位置关系,并说明理由; .
.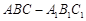 中,
中,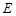 ,
,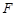 分别为
分别为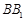 ,
,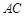 的中点.
的中点.
 平面
平面 ;
;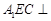 平面
平面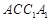 .
.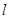 不平行于平面
不平行于平面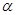 ,且
,且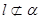 ,则( )
,则( ) 中,过对角线
中,过对角线 的一个平面交棱
的一个平面交棱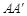 于E,交棱
于E,交棱 于F,则:①四边形
于F,则:①四边形 一定是平行四边形;②四边形
一定是平行四边形;②四边形 .
. ,平面
,平面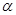 .则“
.则“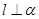 ”是“
”是“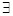 直线
直线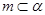 ,
,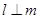 ”的( )
”的( )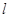 表示一条直线,
表示一条直线,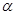 ,
,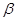 表示两个不重合的平面,有以下三个语句:①
表示两个不重合的平面,有以下三个语句:①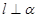 ;②
;②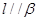 ;③
;③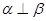 .以其中任意两个作为条件,另外一个作为结论,可以得到三个命题,其中正确命题的个数是( )
.以其中任意两个作为条件,另外一个作为结论,可以得到三个命题,其中正确命题的个数是( )
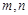 是两条不重合的直线,
是两条不重合的直线,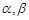 是两个不重合的平面,给出下列命题:
是两个不重合的平面,给出下列命题: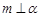 ,
,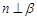 ,且
,且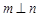 ,则
,则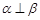 ;
;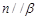 ,且
,且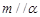 ,
,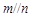 ,则
,则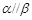 ;
;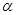 不垂直平面
不垂直平面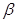 ,那么平面
,那么平面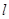 不平行平面
不平行平面