题目内容
(本小题满分14分)
已知:数列{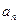 }的前n项和为
}的前n项和为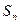 ,满足
,满足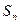 =
=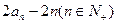
(Ⅰ)证明数列{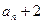 }是等比数列.并求数列{
}是等比数列.并求数列{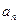 }的通项公式
}的通项公式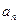 =?
=?
(Ⅱ)若数列{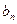 }满足
}满足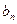 =log2(
=log2(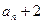 ),而
),而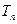 为数列
为数列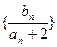 的前n项和,求
的前n项和,求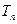 =?
=?
已知:数列{
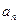 }的前n项和为
}的前n项和为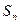 ,满足
,满足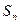 =
=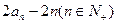
(Ⅰ)证明数列{
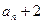 }是等比数列.并求数列{
}是等比数列.并求数列{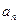 }的通项公式
}的通项公式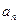 =?
=?(Ⅱ)若数列{
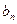 }满足
}满足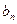 =log2(
=log2(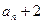 ),而
),而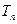 为数列
为数列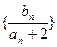 的前n项和,求
的前n项和,求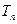 =?
=?(Ⅰ)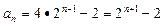
(Ⅱ)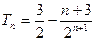
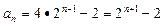
(Ⅱ)
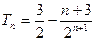
解:(Ⅰ)当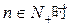 ,
,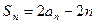 ,①
,①
则当n≥2,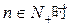 ,
,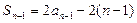 . ②
. ②
①-②,得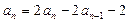 ,
,
即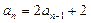 ,………………………2分
,………………………2分
∴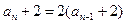 ∴
∴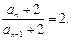 ………………………4分
………………………4分
当n="1" 时,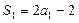 ,则
,则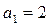 ,
,
∴ {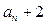 }是以
}是以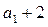 为首项,以2为公比的等比数列. ………………5分
为首项,以2为公比的等比数列. ………………5分
∴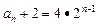 , ∴
, ∴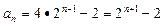 ,…………6分
,…………6分
(Ⅱ)由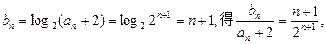 ……………8分
……………8分
则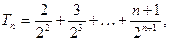 ③ ……………………9分
③ ……………………9分
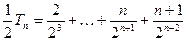 , ④ ……………………10分
, ④ ……………………10分
③-④,得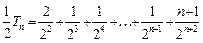 ………………………11分
………………………11分
=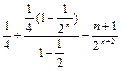 ………………………12分
………………………12分
=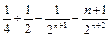 =
= ………………………13分
………………………13分
故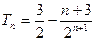 ………………………14分
………………………14分
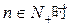 ,
,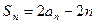 ,①
,①则当n≥2,
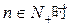 ,
,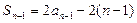 . ②
. ② ①-②,得
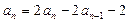 ,
,即
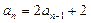 ,………………………2分
,………………………2分∴
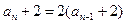 ∴
∴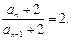 ………………………4分
………………………4分当n="1" 时,
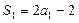 ,则
,则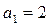 ,
,∴ {
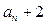 }是以
}是以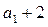 为首项,以2为公比的等比数列. ………………5分
为首项,以2为公比的等比数列. ………………5分∴
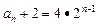 , ∴
, ∴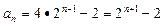 ,…………6分
,…………6分(Ⅱ)由
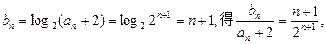 ……………8分
……………8分则
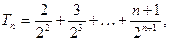 ③ ……………………9分
③ ……………………9分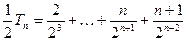 , ④ ……………………10分
, ④ ……………………10分③-④,得
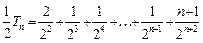 ………………………11分
………………………11分=
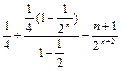 ………………………12分
………………………12分=
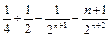 =
= ………………………13分
………………………13分故
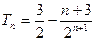 ………………………14分
………………………14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
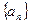 中,
中,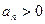 ,其前
,其前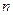 项和为
项和为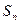 ,
,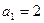 ,且
,且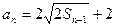
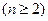 .
.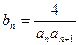 ,求数列
,求数列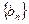 的前
的前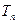 .
.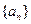 中,
中,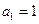 ,当
,当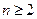 时,其前
时,其前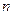 项和
项和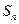 满足
满足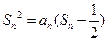 .
.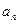 ;
;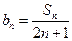 ,求数列
,求数列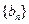 的前项和
的前项和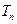 .
.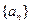 中,
中,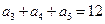 ,则
,则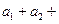 。。。
。。。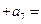 ( )
( )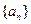 中,
中,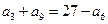 ,
, 表示数列
表示数列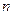 项和,则
项和,则 ( )
( )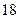


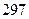
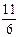
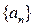 中,
中,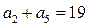 ,
, ,则
,则 ________
________ 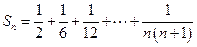 ,且
,且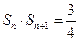 ,则
,则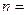 .
.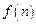 为
为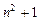
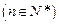 的各位数字之和,如:
的各位数字之和,如: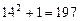 ,
,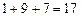 ,则
,则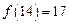 ;记
;记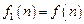 ,
,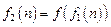 ,
, ,
,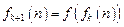 ,
,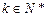 ,则
,则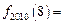 ( )
( )