题目内容
18.已知向量$\overrightarrow{m}$=(sinx,-1),$\overrightarrow{n}$=(cosx,3).(1)当$\overrightarrow{m}$∥$\overrightarrow{n}$,求$\frac{sinx+cosx}{3sinx-2cosx}$的值;
(2)设函数f(x)=($\overrightarrow{m}$+$\overrightarrow{n}$)•$\overrightarrow{m}$,求f(x)的单调增区间;
(3)对于(2)中的f(x),当x∈(0,$\frac{π}{2}$),求f(x)的值域.
分析 (1)利用向量共线的条件,可得3sinx=-cosx,代入,即可得到结论;
(2)利用向量数量积公式化简函数,结合正弦函数的单调增区间,可得f(x)的单调增区间;
(3)求出(2x-$\frac{π}{4}$)的范围,从而确定f(x)的范围,化简函数,可得函数的值域.
解答 解:(1)∵向量$\overrightarrow{m}$=(sinx,-1),$\overrightarrow{n}$=(cosx,3),$\overrightarrow{m}$∥$\overrightarrow{n}$,
∴3sinx=-cosx,
∴$\frac{sinx+cosx}{3sinx-2cosx}$=$\frac{sinx-3sinx}{3sinx+6sinx}$=-$\frac{2}{9}$;
(2)函数f(x)=($\overrightarrow{m}$+$\overrightarrow{n}$)•$\overrightarrow{m}$=(sinx+cosx,2)•(sinx,-1)=sin2x+sinxcosx-2
=$\frac{1-cos2x}{2}$+$\frac{1}{2}$sin2x-2=$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{4}$)-$\frac{3}{2}$,
由2kπ-$\frac{π}{2}$≤2x-$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,可得kπ-$\frac{π}{8}$≤x≤kπ+$\frac{3π}{8}$,
∴f(x)的单调增区间为[kπ-$\frac{π}{8}$,kπ+$\frac{3π}{8}$](k∈Z);
(3)函数f(x)=$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{4}$)-$\frac{3}{2}$,x∈(0,$\frac{π}{2}$),
∴2x-$\frac{π}{4}$∈(-$\frac{π}{4}$,$\frac{3π}{4}$),
∴-$\frac{\sqrt{2}}{2}$<sin(2x-$\frac{π}{4}$)≤1,
∴f(x)的最小值是-2,f(x)的最大值是$\frac{\sqrt{2}-3}{2}$.
点评 本题考查向量知识的运用,考查三角函数的化简,考查学生分析解决问题的能力,属于中档题.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案| A. | 函数的最小正周期为$\frac{π}{2}$ | B. | 函数关于($\frac{π}{6}$,0)中心对称 | ||
| C. | 函数在-$\frac{π}{12}$处取得最大值 | D. | 函数在(-$\frac{π}{12}$,$\frac{π}{6}$)单调递减 |
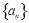 中,
中,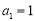 ,
,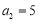 ,
,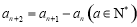 ,则
,则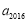 的值为 .
的值为 .