题目内容
1.已知等比数列{an}的前n项和为Sn,S3=$\frac{7}{2}$,S6=$\frac{63}{2}$.(1)求数列{an}的通项公式an;
(2)令bn=6n-61+log2an,求数列{bn}的前n项和为Tn.
分析 (1)通过S3=$\frac{7}{2}$与S6=$\frac{63}{2}$相除可得公比q=2,进而计算可得结论;
(2)通过an=2n-2及对数的性质可知bn=7n-63,利用等差数列的求和公式计算即得结论.
解答 解:(1)∵S3=$\frac{7}{2}$,S6=$\frac{63}{2}$,
∴q≠1,
∴$\frac{{a}_{1}(1-{q}^{3})}{1-q}$=$\frac{7}{2}$,$\frac{{a}_{1}(1-{q}^{6})}{1-q}$=$\frac{63}{2}$,
两式相除得:1+q3=9,解得q=2,
∴a1=$\frac{1}{2}$,
∴an=$\frac{1}{2}$•2n-1=2n-2;
(2)∵an=2n-2,
∴bn=6n-61+log2an
=6n-61+$lo{g}_{2}{2}^{n-2}$
=7n-63,
∴bn+1-bn=[7(n+1)-63]-(7n-63)=7,
∴数列{bn}是首项为-56、公差为7的等差数列,
∴数列{bn}的前n项和为Tn=$\frac{n(-56+7n-63)}{2}$=$\frac{7{n}^{2}-119n}{2}$.
点评 本题考查数列的通项及前n项和,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
10.对于函数y=sin(2x-$\frac{π}{3}$),下列说法正确的是( )
| A. | 函数的最小正周期为$\frac{π}{2}$ | B. | 函数关于($\frac{π}{6}$,0)中心对称 | ||
| C. | 函数在-$\frac{π}{12}$处取得最大值 | D. | 函数在(-$\frac{π}{12}$,$\frac{π}{6}$)单调递减 |
11.已知过点A(a,1)可以作两条直线与圆C:(x-1)2+y2=5相切,则实数a的取值范围是( )
| A. | (-∞,-1) | B. | (-1,3) | C. | [3,+∞) | D. | (-∞,-1)∪(3,+∞) |
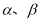 和两条不重合的直线
和两条不重合的直线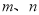 ,则下列四个命题中不正确的是( )
,则下列四个命题中不正确的是( )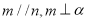 ,则
,则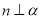
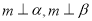 ,则
,则
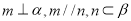 ,则
,则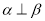
 ,则
,则