题目内容
如图,已知半径为 的⊙
的⊙ 与
与 轴交于
轴交于 、
、 两点,
两点, 为⊙
为⊙ 的切线,切点为
的切线,切点为 ,且
,且 在第一象限,圆心
在第一象限,圆心 的坐标为
的坐标为 ,二次函数
,二次函数 的图象经过
的图象经过 、
、 两点.
两点.
(1)求二次函数的解析式;
(2)求切线 的函数解析式;
的函数解析式;
(3)线段 上是否存在一点
上是否存在一点 ,使得以
,使得以 、
、 、
、 为顶点的三角形与
为顶点的三角形与 相似.若存在,请求出所有符合条件的点
相似.若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(1)二次函数的解析式为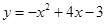 ;(2)切线
;(2)切线 的函数解析式为
的函数解析式为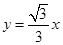 ;
;
(3)点 的坐标为
的坐标为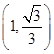 或
或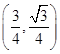 .
.
解析试题分析:(1)先求出圆 的方程,并求出圆
的方程,并求出圆 与
与 轴的交点
轴的交点 和
和 的坐标,然后将点
的坐标,然后将点 和
和 的坐标代入二次函数
的坐标代入二次函数 中解出
中解出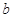 和
和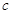 的值,从而确定二次函数的解析式;(2)由于切线
的值,从而确定二次函数的解析式;(2)由于切线 过原点,可设切线
过原点,可设切线 的函数解析式为
的函数解析式为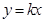 ,利用直线
,利用直线 与圆
与圆 求出
求出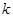 值,结合点
值,结合点 的位置确定切线
的位置确定切线 的函数解析式;(3)对
的函数解析式;(3)对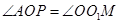 或
或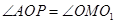 进行分类讨论,充分利用几何性质,从而确定点
进行分类讨论,充分利用几何性质,从而确定点 的坐标.
的坐标.
试题解析:(1)由题意知,圆 的方程为
的方程为 ,令
,令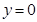 ,解得
,解得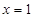 或
或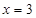 ,
,
故点 的坐标为
的坐标为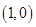 ,点
,点 的坐标为
的坐标为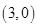 ,
,
由于二次函数 经过
经过 、
、 两点,则有
两点,则有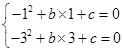 ,解得
,解得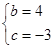 ,
,
故二次函数的解析式为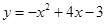 ;
;
(2)设直线 所对应的函数解析式为
所对应的函数解析式为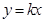 ,由于点
,由于点 在第一象限,则
在第一象限,则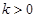 ,
,
由于直线 与圆
与圆 相切,则
相切,则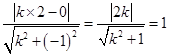 ,解得
,解得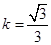 ,
,
故切线 的函数解析式为
的函数解析式为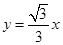 ;
;
(3)由图形知,在 中,
中,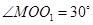 ,
,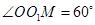 ,
,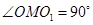 ,
,
在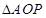 中,
中,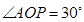 ,由于
,由于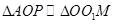 ,因为
,因为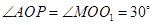 ,
,
则必有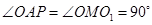 或
或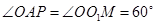 ,
,
联立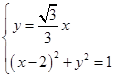 ,解得
,解得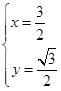 ,故点
,故点 的坐标为
的坐标为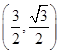 ,
,
当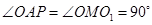 时,直线
时,直线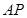 的方程为
的方程为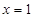 ,联立
,联立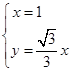 ,于是点
,于是点 的坐标为
的坐标为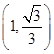 ;
;
当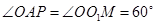 时,
时, ,由于点
,由于点 为线段
为线段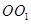 的中点,故点
的中点,故点 为线段
为线段 的中点,
的中点,
此时点 的坐标为
的坐标为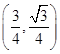 .
.
综上所述,当点 的坐标为
的坐标为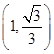

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
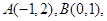 动点P满足
动点P满足 .
.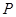 的轨迹为曲线
的轨迹为曲线 ,求此曲线的方程;
,求此曲线的方程; 在直线
在直线 :
: 上,直线
上,直线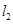 经过点
经过点 ,求
,求 的最小值.
的最小值.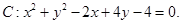 问在圆C上是否存在两点A,B关于直线
问在圆C上是否存在两点A,B关于直线 对称,且以AB为直径的圆经过原点?若存在,写出直线AB的方程,若不存在,说明理由.
对称,且以AB为直径的圆经过原点?若存在,写出直线AB的方程,若不存在,说明理由. ,直线
,直线 ,
, 。
。 取什么实数,直线
取什么实数,直线 与圆恒交于两点;
与圆恒交于两点; 截得的弦长最小时
截得的弦长最小时 的内心为
的内心为 ,过点
,过点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,点
,点 为内切圆
为内切圆 的切点.
的切点.
 四点共圆;
四点共圆; ,求
,求 的度数.
的度数. 截得的弦长是6.
截得的弦长是6. 中,圆
中,圆 的参数方程为
的参数方程为 (
(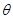 为参数),以
为参数),以 为极轴建立极坐标系,直线
为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 .
. :
: 交
交 轴于
轴于 两点,曲线
两点,曲线 是以
是以 为长轴,直线:
为长轴,直线: 为准线的椭圆.
为准线的椭圆.
 是直线上的任意一点,以
是直线上的任意一点,以 为直径的圆
为直径的圆 与圆
与圆 两点,求证:直线
两点,求证:直线 必过定点
必过定点 ,并求出点
,并求出点 两点,且
两点,且 ,试求此时弦
,试求此时弦