题目内容
如图,锐角 的内心为
的内心为 ,过点
,过点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,点
,点 为内切圆
为内切圆 与边
与边 的切点.
的切点.
(Ⅰ)求证: 四点共圆;
四点共圆;
(Ⅱ)若 ,求
,求 的度数.
的度数.
(Ⅰ)见解析;(Ⅱ)∠DEF=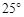 .
.
解析试题分析:(Ⅰ)根据 作直线
作直线 的垂线,垂足为
的垂线,垂足为 得到
得到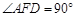 ,由点
,由点 为内切圆
为内切圆 与边
与边 的切点可得
的切点可得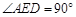 ,根据圆内接四边形的性质与判定可得
,根据圆内接四边形的性质与判定可得 四点共圆;(Ⅱ)根据(Ⅰ)的结论,可知
四点共圆;(Ⅱ)根据(Ⅰ)的结论,可知 =∠DAF,然后根据内心的性质求出
=∠DAF,然后根据内心的性质求出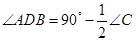 ,然后再直角三角形ADF中,求出
,然后再直角三角形ADF中,求出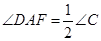 ,即可得出结果.
,即可得出结果.
试题解析:(Ⅰ)由圆D与边AC相切于点E,得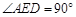 ,
,
∵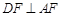 ,得
,得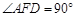 ,∴
,∴ 四点共圆.
四点共圆.
(Ⅱ)由(Ⅰ)知四点 共圆,得∠DEF=∠DAF,
共圆,得∠DEF=∠DAF,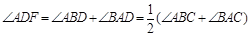
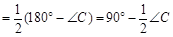 ,
,
结合BF⊥AF,得∠DEF=∠DAF=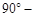 ∠ADF=
∠ADF=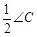 ,∴
,∴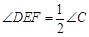 .
.
由 得∠DEF=
得∠DEF=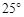 .
.
考点:1.圆内接四边形的性质与判定;2.三角形内心的性质.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 的离心率为
的离心率为 ,且经过点
,且经过点 ,圆
,圆 的直径为
的直径为 的长轴.如图,
的长轴.如图, 是椭圆短轴端点,动直线
是椭圆短轴端点,动直线 过点
过点 两点,
两点, 垂直于
垂直于 .
.
 面积的最大值,并求此时直线
面积的最大值,并求此时直线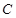 的方程为
的方程为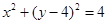 ,点
,点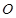 是坐标原点.直线
是坐标原点.直线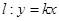 与圆
与圆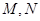 两点.
两点.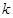 的取值范围;
的取值范围;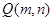 是线段
是线段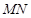 上的点,且
上的点,且 .请将
.请将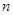 表示为
表示为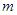 的函数.
的函数. 的圆心在点
的圆心在点 , 点
, 点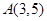 ,求;
,求; 的圆的切线方程;
的圆的切线方程; 点是坐标原点,连结
点是坐标原点,连结 ,
, ,求
,求 的面积
的面积 .
. 的⊙
的⊙ 与
与 轴交于
轴交于 、
、 两点,
两点, 为⊙
为⊙ ,且
,且 ,二次函数
,二次函数 的图象经过
的图象经过
 ,使得以
,使得以 、
、 相似.若存在,请求出所有符合条件的点
相似.若存在,请求出所有符合条件的点
 ,圆
,圆 ,动圆
,动圆 与已知两圆都外切.
与已知两圆都外切. 的方程(2)直线
的方程(2)直线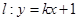 与点
与点 、
、 ,
, 的中垂线与
的中垂线与 轴交于点
轴交于点 ,求点
,求点 ,直线
,直线 与圆
与圆 相交于
相交于 两点,且A点在第一象限.
两点,且A点在第一象限. ;
; (
( )是圆
)是圆 关于原点的对称点为
关于原点的对称点为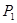 ,点
,点 轴的对称点为
轴的对称点为 ,如果直线
,如果直线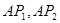 与
与 轴分别交于
轴分别交于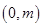 和
和 .问
.问 是否为定值?若是,求出定值,若不是,说明理由.
是否为定值?若是,求出定值,若不是,说明理由.  过点
过点 ,且与直线
,且与直线 相切于点
相切于点 .
.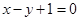 对称的圆
对称的圆 的方程.
的方程.