题目内容
【题目】已知函数 
的最小值为 
．
（1）求 
的值；（2）求 
的解析式．
【答案】（1）-4；（2）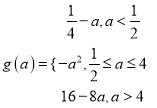
【解析】试题分析：（1）由a=2，求得f（t）=（t﹣2）2﹣4，即可得到最小值g（2）；
（2）运用换元法和二次函数的对称轴和区间的关系，对a展开讨论，即可得到最小值的表达式．
试题解析：
（1）a=2时，f（x）=4x﹣42x（﹣1≤x≤2）
=（2x﹣2）2﹣4，
令t=2x（
≤t≤4），
即有f（t）=（t﹣2）2﹣4，
由于2∈[，4]，可得最小值g（2）=﹣4；
（2）函数f（x）=4x﹣a2x+1（﹣1≤x≤2），
令t=2x（≤t≤4），
则f（t）=t2﹣2at=（t﹣a）2﹣a2，
当a≤时，区间[，4]为增区间，即有t=取得最小值
﹣a；
当＜a＜4时，当t=a时，取得最小值﹣a2；
当a≥4时，区间[，4]为减区间，即有t=4取得最小值16﹣8a．
即有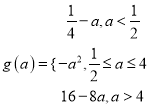
．
练习册系列答案
相关题目
