题目内容
本小题满分12分)设函数 ,当点
,当点 是函数
是函数 图象上的点
图象上的点 时,点
时,点 是函数
是函数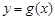 图象上的点.
图象上的点.
(1)写出函数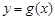 的解析式;
的解析式;
(2)若当 时,恒有
时,恒有 ,试确定
,试确定 的取值范围;
的取值范围;
(3)把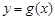 的图象向左平移
的图象向左平移 个单位得到
个单位得到 的图象,函数
的图象,函数
 ,(
,( )在
)在 的最大值为
的最大值为 ,求
,求 的值
的值
 ,当点
,当点 是函数
是函数 图象上的点
图象上的点 时,点
时,点 是函数
是函数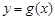 图象上的点.
图象上的点.(1)写出函数
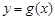 的解析式;
的解析式;(2)若当
 时,恒有
时,恒有 ,试确定
,试确定 的取值范围;
的取值范围;(3)把
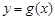 的图象向左平移
的图象向左平移 个单位得到
个单位得到 的图象,函数
的图象,函数
 ,(
,( )在
)在 的最大值为
的最大值为 ,求
,求 的值
的值解:(1)设点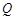 的
的 坐标为
坐标为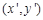 ,则
,则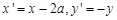 ,即
,即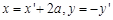 。
。
∵点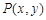 在函数
在函数 图象上
图象上
∴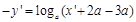 ,即
,即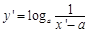
∴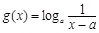
(2)由题意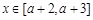 ,则
,则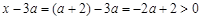 ,
,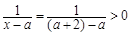 .
.
又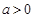 ,且
,且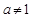 ,∴
,∴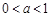
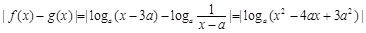
∵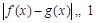 ∴
∴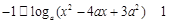 ,
,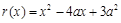 对称轴为
对称轴为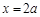
∵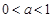 ∴
∴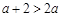 ,则
,则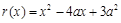 在
在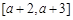 上为增函数,
上为增函数,
∴函数 在
在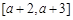 上为减函数,
上为减函数,
从而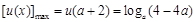 。
。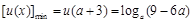
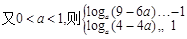
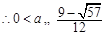
(3)由(1)知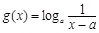 ,而把
,而把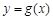 的图象向左平移
的图象向左平移 个单位得到
个单位得到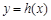 的图象,则
的图象,则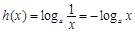 ,
,
∴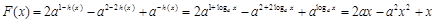 ,
,
即 ,又
,又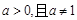 ,
,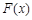 的对称轴为
的对称轴为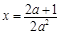 ,又在
,又在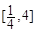 的最大值为
的最大值为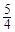 ,
,
①令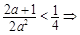
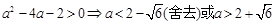 ;此时
;此时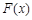 在
在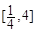 上递减,∴
上递减,∴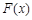 的最大值为
的最大值为
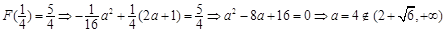 ,此时无解;
,此时无解;
②令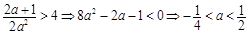 ,又
,又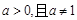 ,∴
,∴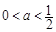 ;此时
;此时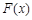 在
在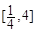 上递增,∴
上递增,∴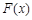 的最大值为
的最大值为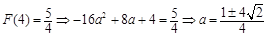 ,又
,又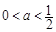 ,∴无解;
,∴无解;
③令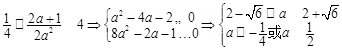 且
且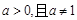
∴ ,此时
,此时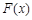 的最大值为
的最大值为
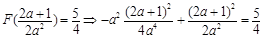
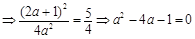 ,
,
解得: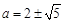 ,又
,又 ,∴
,∴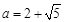 ;
;
综上, 的值为
的值为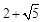 .
.
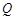 的
的 坐标为
坐标为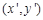 ,则
,则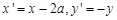 ,即
,即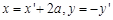 。
。∵点
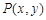 在函数
在函数 图象上
图象上∴
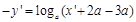 ,即
,即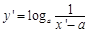
∴
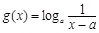
(2)由题意
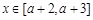 ,则
,则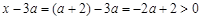 ,
,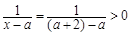 .
.又
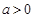 ,且
,且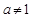 ,∴
,∴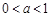
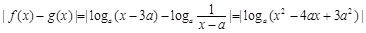
∵
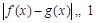 ∴
∴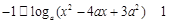 ,
,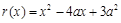 对称轴为
对称轴为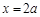
∵
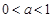 ∴
∴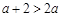 ,则
,则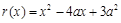 在
在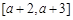 上为增函数,
上为增函数,∴函数
 在
在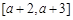 上为减函数,
上为减函数,从而
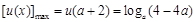 。
。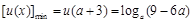
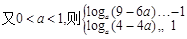
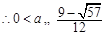
(3)由(1)知
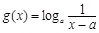 ,而把
,而把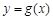 的图象向左平移
的图象向左平移 个单位得到
个单位得到 的图象,则
的图象,则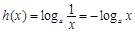 ,
,∴
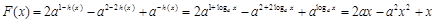 ,
,即
 ,又
,又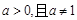 ,
,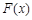 的对称轴为
的对称轴为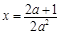 ,又在
,又在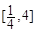 的最大值为
的最大值为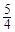 ,
,①令
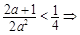
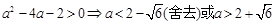 ;此时
;此时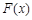 在
在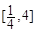 上递减,∴
上递减,∴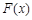 的最大值为
的最大值为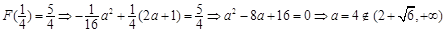 ,此时无解;
,此时无解;②令
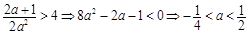 ,又
,又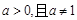 ,∴
,∴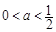 ;此时
;此时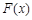 在
在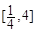 上递增,∴
上递增,∴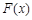 的最大值为
的最大值为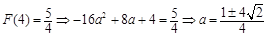 ,又
,又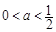 ,∴无解;
,∴无解;③令
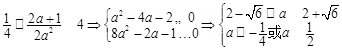 且
且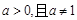
∴
 ,此时
,此时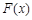 的最大值为
的最大值为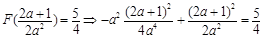
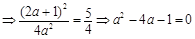 ,
,
解得:
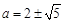 ,又
,又 ,∴
,∴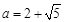 ;
;综上,
 的值为
的值为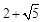 .
.略

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 的背面靠墙的猪圈, 底面为长方形的猪圈正面的造价为120元/
的背面靠墙的猪圈, 底面为长方形的猪圈正面的造价为120元/ , 且不计猪圈背面的费用, 问怎样设计能使猪圈的总造价最低, 最低总造价是多少元?
, 且不计猪圈背面的费用, 问怎样设计能使猪圈的总造价最低, 最低总造价是多少元? 的不等式
的不等式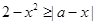 至少有一个负数解,则
至少有一个负数解,则 的最小值为_______.
的最小值为_______. =
= 的值域是 ( )
的值域是 ( ) 成立,则称f(x)[a,b]上的凸函数。试问:在下列图像中,是凸函数图像的为
成立,则称f(x)[a,b]上的凸函数。试问:在下列图像中,是凸函数图像的为
 g(x)=
g(x)= ,则函数h(x)= f (x)·g(x)
,则函数h(x)= f (x)·g(x) 时小白鼠将会死亡,注射这种抗癌药物可杀死其体内癌细胞的
时小白鼠将会死亡,注射这种抗癌药物可杀死其体内癌细胞的 .
.

 是定义在R上的奇函数,当
是定义在R上的奇函数,当 时,
时, ,则不等式
,则不等式 的解集是
的解集是



 ,则其解析式为
,则其解析式为