题目内容
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ≌
≌![]() ,
,![]() ,
,![]() 是线段
是线段![]() 的中点.
的中点.
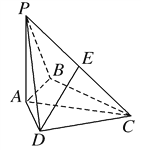
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:![]() 建立空间直角坐标系,给出相应点坐标,得平面PAB的法向量为
建立空间直角坐标系,给出相应点坐标,得平面PAB的法向量为![]() ,由
,由![]() ,即可得
,即可得![]() ∥平面
∥平面![]()
![]() 求出平面
求出平面![]() 的一个法向量,平面
的一个法向量,平面![]() 的法向量,利用向量的夹角公式,即可求出二面角
的法向量,利用向量的夹角公式,即可求出二面角![]() 的余弦值;
的余弦值;
解析:(1)证明:以B为坐标原点,BA所在的直线为x轴,BC所在的直线为y轴,过点B且与平面ABC垂直的直线为z轴,建立空间直角坐标系如图所示.

则B(0,0,0),C(0,![]() ,0),P(1,0,2),D
,0),P(1,0,2),D![]() ,A(1,0,0),E
,A(1,0,0),E![]() ,∴
,∴![]() ,
,![]() ,
,![]() .
.
显然平面PAB的法向量为![]() ,由
,由![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() ∥平面
∥平面![]() .
.
(2)由(1)知![]() ,
,![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,则
,则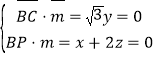 ,取
,取![]() ,则
,则![]() ,∴
,∴![]() 为平面
为平面![]() 的一个法向量.同理:平面
的一个法向量.同理:平面![]() 的法向量为
的法向量为![]()
∴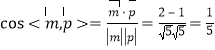 ,故二面角
,故二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】已知函数f(x)=|x+ ![]() |﹣|x﹣
|﹣|x﹣ ![]() |;
|;
(1)作出函数f(x)的图象;
(2)根据(1)所得图象,填写下面的表格:
性质 | 定义域 | 值域 | 单调性 | 奇偶性 | 零点 |
f(x) |
(3)关于x的方程f2(x)+m|f(x)|+n=0(m,n∈R)恰有6个不同的实数解,求n的取值范围. 
