题目内容
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,且
是直角梯形,且![]()
![]() ,
,![]() .
.
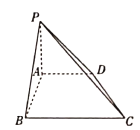
(1)证明:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)推导出PA⊥AD,PA⊥AB,由此能证明PA⊥平面ABCD.(2)以A为原点,AB,AD,AP为x,y,z轴的正方向建立空间直角坐标系,利用向量法能求出平面PBC与平面PAD所成锐二面角的余弦值.
(1)因为![]() ,所以
,所以![]() ,即
,即![]() .
.
同理可得![]() .
.
因为![]() .所以
.所以![]() 平面
平面![]() .
.
(2)由题意可知,![]() 两两垂直,故以A为原点,
两两垂直,故以A为原点,![]() 分别为
分别为![]() 轴的正方向建立如图所示的空间直角坐标系,
轴的正方向建立如图所示的空间直角坐标系,
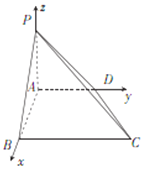
则![]() ,
,
所以![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则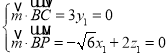 ,
,
不妨取![]() 则
则![]()
易得![]() 平面
平面![]() ,所以平面
,所以平面![]() 的一个法向量为
的一个法向量为![]() ,
,
记平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,则
,则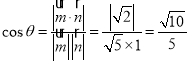
故平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
【题目】下表表示的是某款车的车速与刹车距离的关系,试分别就![]() ,
,![]() ,
,![]() 三种函数关系建立数学模型,并探讨最佳模拟,根据最佳模拟求车速为120km/h时的刹车距离.
三种函数关系建立数学模型,并探讨最佳模拟,根据最佳模拟求车速为120km/h时的刹车距离.
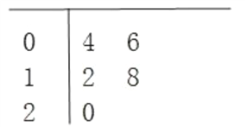
车速/(km/h) | 10 | 15 | 30 | 40 | 50 |
刹车距离/m | 4 | 7 | 12 | 18 | 25 |
车速/((km/h) | 60 | 70 | 80 | 90 | 100 |
刹车距离/m | 34 | 43 | 54 | 66 | 80 |