题目内容
【题目】已知数列![]() 中,
中,![]() ,且
,且![]() .
.
(1)求证:![]() 是等比数列,并求数列
是等比数列,并求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 中是否存在不同的三项按照一定顺序重新排列后,构成等差数列?若存在,求满足条件的项;若不存在,说明理由.
中是否存在不同的三项按照一定顺序重新排列后,构成等差数列?若存在,求满足条件的项;若不存在,说明理由.
【答案】(1)证明见解析,![]() ;(2)不存在.
;(2)不存在.
【解析】
(1)推导出an+1+1=﹣3(an+1),n∈N*.a1+1=2,由此能证明{an+1}是以2为首项,﹣3为公比的等比数列,可求数列{an}通项公式.(2)假设am,an,ap构成等差数列,m≠n≠p,则2an=am+ap,利用(1)的通项公式进行推导不满足2an=am+ap,从而数列{an}中不存在不同的三项按照一定顺序重新排列后,构成等差数列.
(1)因为![]() ,所以
,所以![]() ,因为
,因为![]() ,
,
所以数列![]() 是以2为首项,以-3为公比的等比数列,
是以2为首项,以-3为公比的等比数列,
所以![]() ,即
,即![]() ;
;
(2)假设存在三项![]() 按一定顺序重新排列后成等差.
按一定顺序重新排列后成等差.
①若![]() ,则
,则![]() ,
,
整理得![]() ,两边同除以
,两边同除以![]() ,
,
可得![]() ,
,
等式右边是-3的整数倍,左边不是-3的整数倍,故等式不成立.
②若![]() ,则
,则![]() ,
,
整理得![]() ,两边同除以
,两边同除以![]() ,
,
可得![]() ,
,
等式右边是-3的整数倍,左边不是-3的整数倍,故等式不成立.
③若![]() ,则
,则![]() ,
,
整理得![]() ,两边同除以
,两边同除以![]() ,
,
可得![]() ,
,
等式左边是-3的整数倍,右边不是-3的整数倍,故等式不成立;
综上,不存在不同的三项符合题意.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案【题目】在一次恶劣气候的飞行航程中调查男女乘客在飞机上晕机的情况,共调查了89位乘客,其中男乘客有24人晕机,31人不晕机;女乘客有8人晕机,26人不晕机
(1)根据此材料数据完成如下的2×2列联表;
晕机 | 不晕机 | 总计 | |
男人 | |||
女人 | |||
总计 |
(2)根据列联表,利用下列公式和数据分析,你是否有90%的把握认为在本次飞机飞行中晕机与性别有关?
(3)其中8名晕机的女乘客中有5名是常坐飞机的乘客,另外3名是不常坐飞机的,从这8名乘客中任选3名,这3名乘客不都是常坐飞机的概率是多少?
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
参考公式: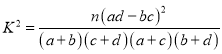 ,其中
,其中![]()