题目内容
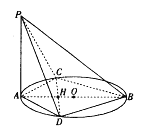
【题目】已知点
为抛物线
的焦点，点
在抛物线
上，且
．
（1）求抛物线的方程；
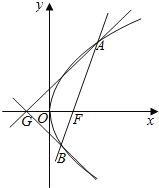
（2）已知点
，延长
交抛物线于点
，证明：以点为圆心且与直线
相切的圆，必与直线
相切．
【答案】（1）
；（2）详见解析
【解析】
（1）由抛物线定义可得：
，解得
．即可得出抛物线
的方程．
（2）由点
在抛物线上，解得
，不妨取
，
，
，可得直线
的方程，与抛物线方程联立化为
，解得
，
．又
，计算
，
，可得
，
，即可证明以点
为圆心且与直线
相切的圆，必与直线
相切．
（1）解：由抛物线定义可得：，解得
．
抛物线的方程为；
（2）证明：
点在抛物线上，
，解得
，不妨取，，，
直线的方程：
，
联立抛物线，化为，解得
或
，，．
又，
．
，
，
，
轴平分
，
因此点到直线，的距离相等，
以点为圆心且与直线相切的圆，必与直线相切．
练习册系列答案
相关题目
