题目内容
(本小题满分13分)已知函数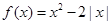 .
.
(Ⅰ)判断并证明函数的奇偶性;
(Ⅱ)判断函数 在
在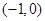 上的单调性并加以证明.
上的单调性并加以证明.
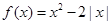 .
.(Ⅰ)判断并证明函数的奇偶性;
(Ⅱ)判断函数
 在
在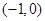 上的单调性并加以证明.
上的单调性并加以证明. 解(Ⅰ)是偶函数.见解析;(Ⅱ)是单调递增函数.见解析。
本试题主要是考查了函数的奇偶性和函数的单调性的运用。
(1)因为定义域为实数集,且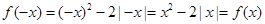 ,那么可知函数为偶函数。
,那么可知函数为偶函数。
(2)利用定义法,作差变形定号, 下结论可知函数在给定区间上是增函数。
解(Ⅰ)是偶函数. …………………………………………………………………2分
定义域是R,
∵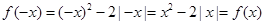
∴ 函数 是偶函数. ……………………………………………………………6分
是偶函数. ……………………………………………………………6分
(直接证明得正确结论给6分)
(Ⅱ)是单调递增函数. ……………………………………………………………8分
当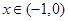 时,
时,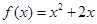
设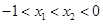 ,则
,则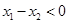 ,且
,且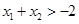 ,即
,即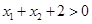
∵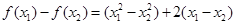
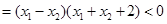 ………………………………………12分
………………………………………12分
∴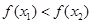
所以函数 在
在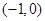 上是单调递增函数.………………………13分
上是单调递增函数.………………………13分
(1)因为定义域为实数集,且
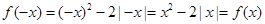 ,那么可知函数为偶函数。
,那么可知函数为偶函数。(2)利用定义法,作差变形定号, 下结论可知函数在给定区间上是增函数。
解(Ⅰ)是偶函数. …………………………………………………………………2分
定义域是R,
∵
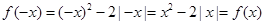
∴ 函数
 是偶函数. ……………………………………………………………6分
是偶函数. ……………………………………………………………6分(直接证明得正确结论给6分)
(Ⅱ)是单调递增函数. ……………………………………………………………8分
当
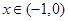 时,
时,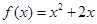
设
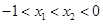 ,则
,则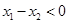 ,且
,且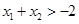 ,即
,即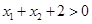
∵
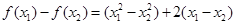
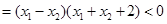 ………………………………………12分
………………………………………12分∴
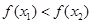
所以函数
 在
在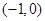 上是单调递增函数.………………………13分
上是单调递增函数.………………………13分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
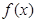 与
与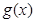 的定义域是
的定义域是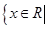
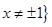 ,函数
,函数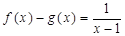 ,则
,则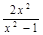
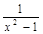

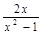
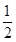 对称,且f′(1)=0.
对称,且f′(1)=0.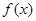 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当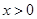 时,
时,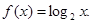 已知a="f" (4),b="f" (
已知a="f" (4),b="f" (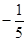 ),c="f" (
),c="f" (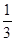 ),则
),则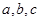 的大小关系为______.(用“
的大小关系为______.(用“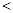 ”连结)
”连结) 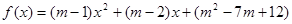 为偶函数,则
为偶函数,则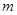 =( )
=( )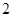
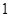
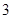
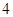
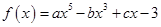 ,
,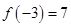 ,则
,则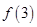 的值为 ___________
的值为 ___________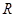 上的函数
上的函数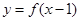 的图像关于
的图像关于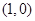 对称,且当
对称,且当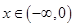 时,
时,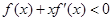 (其中
(其中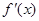 是
是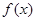 的导函数),若
的导函数),若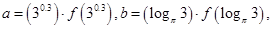
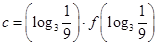 ,则
,则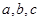 的大小关系是( )
的大小关系是( )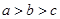
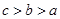
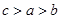
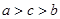
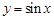
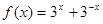 与
与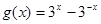 的定义域均为R,则
的定义域均为R,则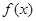 与
与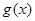 与均为偶函数 B.
与均为偶函数 B.