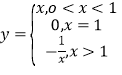Question

【题目】已知圆与直线相切.

（1）求圆的方程；

（2）求直线截圆所得弦的长；

（3）过点作两条直线与圆相切，切点分别为，求直线的方程.

Answer 1

【答案】（1）；（2）；（3）

【解析】分析：（1）设出圆的方程，由直线和圆相切的条件，求得半径，即可得到圆的方程；

（2）求出圆心到直线的距离，运用直线和圆相交的弦长公式，即可得到；

（3）判断出C，M，N，G四点共圆，求出圆的方程，再与圆C方程相减，即可得到相交弦方程．

详解：(1)由题意知，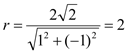

所以圆的方程为

（2）由题意，圆心到的距离 ,

（3）由题意知，

其方程为

又在圆，两式相减得

即直线的方程为.

点晴：本题主要考察直线与圆的位置关系，圆与圆的位置关系，这块内容在解析几何中属于核心内容，学生们需要关注几何方法和代数方法，几何方法需要转化，计算量相对较小，代数方法计算量较大。