题目内容
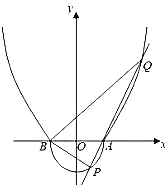
【题目】如图,由半圆![]() 和部分抛物线
和部分抛物线![]() 合成的曲线
合成的曲线![]() 称为“羽毛球开线”,曲线
称为“羽毛球开线”,曲线![]() 与
与![]() 轴有
轴有![]() 两个焦点,且经过点
两个焦点,且经过点![]()
(1)求![]() 的值;
的值;
(2)设![]()
![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的最小值;
的最小值;
(3)过![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与“羽毛球形线”相交于点
与“羽毛球形线”相交于点![]() 三点,问是否存在实数
三点,问是否存在实数![]() 使得
使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,且
;(3)存在,且![]() ,详见解析
,详见解析
【解析】
(1)将![]() 代入
代入![]() 求出
求出![]() ,再由
,再由![]() 与
与![]() 轴交点坐标,代入圆的方程,即可求出
轴交点坐标,代入圆的方程,即可求出![]() ;
;
(2)先设![]() ,得到
,得到![]() ,分别讨论
,分别讨论![]() ,和
,和![]() 两种情况,由抛物线与圆的方程,即可求出结果;
两种情况,由抛物线与圆的方程,即可求出结果;
(3)先由题意得到![]() 的方程,与抛物线联立,求出
的方程,与抛物线联立,求出![]() ;与圆联立,求出
;与圆联立,求出 ,根据
,根据![]() 得到
得到![]() ,化简得到关于
,化简得到关于![]() 的方程,求解,即可得出结果.
的方程,求解,即可得出结果.
(1)由题意,将![]() 代入
代入![]() ,得到
,得到![]() ;所以抛物线
;所以抛物线![]() ;
;
又![]() 与
与![]() 轴交于
轴交于![]() ,所以
,所以![]() ,代入圆的方程,可得
,代入圆的方程,可得![]() ;
;
所以![]() ,
,![]() ;
;
(2)设![]() ,因为
,因为![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
所以![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,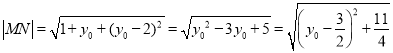 ,
,
所以![]() 时,
时,![]() ;
;
而![]() ,所以
,所以![]() 的最小值为
的最小值为![]() ;
;
(3)由题意,可得:![]() 的方程为
的方程为![]() ,
,
由![]() ,整理得:
,整理得:![]() ,
,
解得![]() 或
或![]() ,即
,即![]() ;
;
由![]() ,整理得:
,整理得:![]()
解得:![]() 或
或![]() ,则
,则 ,
,
由![]() ,可得
,可得![]() ,
,
即 ,整理得
,整理得![]() ,解得
,解得![]() (由题意,负值舍去)
(由题意,负值舍去)
因此,存在实数![]() ,使得
,使得![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某公司培训员工某项技能,培训有如下两种方式:
方式一:周一到周五每天培训1小时,周日测试
方式二:周六一天培训4小时,周日测试
公司有多个班组,每个班组60人,现任选两组![]() 记为甲组、乙组
记为甲组、乙组![]() 先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
先培训;甲组选方式一,乙组选方式二,并记录每周培训后测试达标的人数如表:
第一周 | 第二周 | 第三周 | 第四周 | |
甲组 | 20 | 25 | 10 | 5 |
乙组 | 8 | 16 | 20 | 16 |
![]() 用方式一与方式二进行培训,分别估计员工受训的平均时间
用方式一与方式二进行培训,分别估计员工受训的平均时间![]() 精确到
精确到![]() ,并据此判断哪种培训方式效率更高?
,并据此判断哪种培训方式效率更高?
![]() 在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
在甲乙两组中,从第三周培训后达标的员工中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求这2人中至少有1人来自甲组的概率.
【题目】某校的1000名高三学生参加四门学科的选拔考试,每门试卷共有10道题,每题10分,规定:每门错![]() 题成绩记为
题成绩记为![]() ,错
,错![]() 题成绩记为
题成绩记为![]() ,错
,错![]() 题成绩记为
题成绩记为![]() ,错
,错![]() 题成绩记为
题成绩记为![]() ,在录取时,
,在录取时,![]() 记为90分,
记为90分,![]() 记为80分,
记为80分,![]() 记为60分,
记为60分,![]() 记为50分.
记为50分.
根据模拟成绩,每一门都有如下统计表:
答错 题数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
频数 | 10 | 90 | 100 | 150 | 150 | 200 | 100 | 100 | 50 | 49 | 1 |
已知选拔性考试成绩与模拟成绩基本吻合.
(1)设![]() 为高三学生一门学科的得分,求
为高三学生一门学科的得分,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)预测考生4门总分为320概率.
【题目】某大学生参加社会实践活动,对某公司1月份至6月份销售某种配件的销售量及销售单价进行了调查,销售单价x和销售量y之间的一组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价(元) | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量(件) | 11 | 10 | 8 | 6 | 5 | 14.2 |
(1)根据1至5月份的数据,求出y关于x的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中![]() ,
,![]()