题目内容
【题目】一条光线从点A(3,2)发出,经x轴反射后,通过点B(-1,6),求入射光线和反射光线所在的直线方程.
【答案】解如图所示,作A点关于x轴的对称点A′,显然,A′坐标为(3,-2),连接A′B,则A′B所在直线即为反射光线.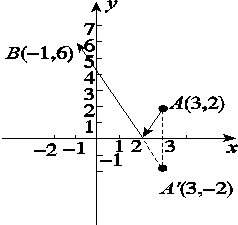
由两点式可得直线A′B的方程为 ![]() ,即2x+y-4=0.
,即2x+y-4=0.
同理,点B关于x轴的对称点为B′(-1,-6),
由两点式可得直线AB′的方程为 ![]() ,即2x-y-4=0,
,即2x-y-4=0,
∴入射光线所在直线方程为2x-y-4=0,
反射光线所在直线方程为2x+y-4=0:
【解析】由光在反射过程中,入射光线与反射光线关于x轴对称,求出点A,B关于x轴的对称点的坐标,即求出了入射光线与反射光线分别过两点,则两点式方程求出直线方程.
【考点精析】利用两点式方程对题目进行判断即可得到答案,需要熟知直线的两点式方程:已知两点![]() 其中
其中![]() 则:y-y1/y-y2=x-x1/x-x2.
则:y-y1/y-y2=x-x1/x-x2.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
