题目内容
【题目】某商场出售两款型号不同的手机，由于市场需求发生变化，第一款手机连续两次提价10%，第二款手机连续两次降价10%，结果都以1210元出售．
(1)求第一款手机的原价；
(2)若该商场同时出售两款手机各一部，求总售价与总原价之间的差额．(结果精确到整数)
【答案】（1）1000元（2）
【解析】试题分析：建立一次函数模型进行求解.（1）设第一款手机原价为
，根据题意写出方程
解得
.（2）设第二款手机原价为
，根据题意写出方程
，解得
，进而可得所求为
.
试题解析：
解：(1)设第一款手机原价为a，则a(1＋10%)2＝1210，
解得a＝
＝1000，所以第一款手机原价为1000元．
(2)设第二款手机原价为b，则b(1－10%)2＝1210，
解得
≈1494元，由(1)知，第一款手机原价为1000元，
所以总售价与总原价之间的差额为1210×2－1494－1000＝－74.
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
【题目】如图所示，在四棱锥P－ABCD中，底面是边长为a的正方形，侧棱PD＝a，PA＝PC＝
a，
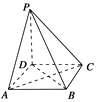
(1)求证：PD⊥平面ABCD；
(2)求证：平面PAC⊥平面PBD；
(3)求二面角P－AC－D的正切值．
【题目】某企业想通过做广告来提高销售额，经预测可知本企业产品的广告费x（单位：百万元）与销售额y（单位：百万元）之间有如下对应数据：
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
由表中的数据得线性回归方程为 
= 
x+ 
，其中 =6.5，由此预测当广告费为7百万元时，销售额为万元．
