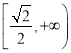题目内容
【题目】已知椭圆C的方程为 ![]() +
+ ![]() =1(a>b>0),双曲线
=1(a>b>0),双曲线 ![]() ﹣
﹣ ![]() =1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4
=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4 ![]() .
.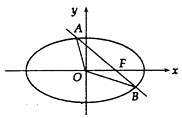
(1)求椭圆C的方程;
(2)过右焦点F的直线l,交椭圆于A、B两点,记△AOF的面积为S1 , △BOF的面积为S2 , 当S1=2S2时,求 ![]()
![]() 的值.
的值.
【答案】
(1)解:由一条渐近线与x轴所成的夹角为30°,则 ![]() =tan30°=
=tan30°= ![]() ,即a2=3b2,
,即a2=3b2,
由2c=4 ![]() .c=2
.c=2 ![]() ,则a2+b2=8,
,则a2+b2=8,
解得:a2=8,b2=2,
∴椭圆的标准方程: ![]()
(2)解:由(1)可知:F(2,0),直线AB的方程:x=ty+2,A(x1,y1),B(x2,y2),
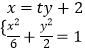 ,整理得:(t2+3)y2+4ty﹣2=0,
,整理得:(t2+3)y2+4ty﹣2=0,
y1+y2=﹣ ![]() ,y1y2=﹣
,y1y2=﹣ ![]() ,
,
由S1=2S2时,则y1=﹣2y2时,解得:t2= ![]() ,
,
将t2= ![]() ,代入y1y2=﹣
,代入y1y2=﹣ ![]() ,
,
x1x2=(ty1+2)(ty2+2)=t2y1y2+2t(y1+y2)+4,
= ![]() ,
,
由 ![]()
![]() =x1x2+y1y2=
=x1x2+y1y2= ![]() ﹣
﹣ ![]() =
= ![]() ,得:
,得:
![]()
![]() =
= ![]()
【解析】(1)由双曲线的渐近线方程及斜率公式,即可求得a2=3b2,c=2 ![]() ,即a2+b2=8,即可求得a和b的值,求得椭圆方程;(2)设直线l的方程,代入椭圆方程,利用韦达定理及y1=﹣2y2,即可求得t的值,分别求得y1y2,x1x2,利用向量数量积的坐标运算,即可求得
,即a2+b2=8,即可求得a和b的值,求得椭圆方程;(2)设直线l的方程,代入椭圆方程,利用韦达定理及y1=﹣2y2,即可求得t的值,分别求得y1y2,x1x2,利用向量数量积的坐标运算,即可求得 ![]()
![]() 的值.
的值.

【题目】某企业想通过做广告来提高销售额,经预测可知本企业产品的广告费x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
由表中的数据得线性回归方程为 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =6.5,由此预测当广告费为7百万元时,销售额为万元.
=6.5,由此预测当广告费为7百万元时,销售额为万元.
【题目】某某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min).下面是这次抽样的频率分布表和频率分布直方图,解答下列问题:
分组 | 频数 | 频率 | |
一组 | 0≤t<5 | 0 | 0 |
二组 | 5≤t<10 | 10 | |
三组 | 10≤t<15 | 10 | 0.10 |
四组 | 15≤t<20 | ||
五组 | 20≤t<25 | 30 | 0.30 |
合计 | 100 | 1.00 | |

(1)这次抽样的样本容量是多少?
(2)在表中填写缺失的数据并补全频率分布直方图.
(3)旅客购票用时的平均数可能落在哪一个小组?
(4)若每增加一个购票窗口可使平均购票用时缩短5 min,要使平均购票用时不超过10 min,那么你估计最少要增加几个窗口?