题目内容
【题目】已知关于x的不等式:|2x﹣m|≤1的整数解有且仅有一个值为2.
(1)求整数m的值;
(2)在(1)的条件下,解不等式:|x﹣1|+|x﹣3|≥m.
【答案】
(1)解:由不等式|2x﹣m|≤1,可得 ![]() ,∵不等式的整数解为2,
,∵不等式的整数解为2,
∴ ![]() ,解得 3≤m≤5.
,解得 3≤m≤5.
再由不等式仅有一个整数解2,∴m=4
(2)解:本题即解不等式|x﹣1|+|x﹣3|≥4,
当x≤1时,不等式等价于 1﹣x+3﹣x≥4,解得 x≤0,不等式解集为{x|x≤0}.
当1<x≤3时,不等式为 x﹣1+3﹣x≥4,解得x∈,不等式解为.
当x>3时,x﹣1+x﹣3≥4,解得x≥4,不等式解集为{x|x≥4}.
综上,不等式解为(﹣∞,0]∪[4,+∞)
【解析】(1)已知关于x的不等式:|2x﹣m|≤1,化简为 ![]() ,再利用不等式整数解有且仅有一个值为2,求出m的值.(2)可以分类讨论,根据讨论去掉绝对值,然后求解.
,再利用不等式整数解有且仅有一个值为2,求出m的值.(2)可以分类讨论,根据讨论去掉绝对值,然后求解.
【考点精析】认真审题,首先需要了解绝对值不等式的解法(含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号).

 阅读快车系列答案
阅读快车系列答案【题目】随着生活水平的提高,人们对空气质量的要求越来越高,某机构为了解公众对“车辆限行”的态度,随机抽查![]() 人,并将调查情况进行整理后制成下表:
人,并将调查情况进行整理后制成下表:
年龄(岁) |
|
|
|
|
|
频数 |
|
|
|
|
|
赞成人数 |
|
|
|
|
|
(1)完成被调查人员年龄的频率分布直方图,并求被调査人员中持赞成态度人员的平均年龄约为多少岁?
(2)若从年龄在![]() 的被调查人员中各随机选取
的被调查人员中各随机选取![]() 人进行调查.请写出所有的基本亊件,并求选取
人进行调查.请写出所有的基本亊件,并求选取![]() 人中恰有
人中恰有![]() 人持不赞成态度的概率.
人持不赞成态度的概率.

【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等极如下表:
质量指标值 |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
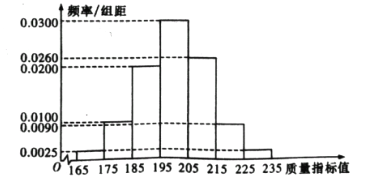
(1)根据以上抽样调查数据 ,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品90%”的规定?
(2)在样本中,按产品等极用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?