题目内容
17.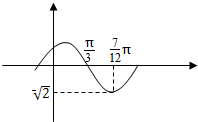 函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,
函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,(1)求函数f(x)的解析式;
(2)解不等式f(x)≤1.
分析 (1)先由图象可得A,然后利用图象求得函数的周期,由周期公式求得ω,最后根据点($\frac{7π}{12}$,-$\sqrt{2}$)在函数图象上,且-$\frac{π}{2}$<φ<$\frac{π}{2}$,求得φ,即可得解.
(2)由题意解$sin(2x+\frac{π}{3})≤\frac{{\sqrt{2}}}{2}$,由正弦函数的图象和性质可得$-\frac{5π}{4}+2kπ≤2x+\frac{π}{3}≤\frac{π}{4}+2kπ,k∈Z$,进一步化简即可得解.
解答 解:(1)∵由图可知$A=\sqrt{2}$,$T=4(\frac{7π}{12}-\frac{π}{3})=π$,
∴$ω=\frac{2π}{π}=2$,
∴可得:$f(x)=\sqrt{2}sin(2x+φ)$,
∵将点$({\frac{7π}{12},-\sqrt{2}})$代入得,$f(\frac{7π}{12})=\sqrt{2}sin(2×\frac{7π}{12}+φ)=-\sqrt{2}$,
∴$\frac{7π}{6}+φ=\frac{3π}{2}+2kπ,k∈Z$,
又$-\frac{π}{2}<φ<\frac{π}{2}$,
∴$φ=\frac{π}{3}$.
∴$f(x)=\sqrt{2}sin(2x+\frac{π}{3})$…(6分)
(2)由f(x)≤1得$sin(2x+\frac{π}{3})≤\frac{{\sqrt{2}}}{2}$,
∴$-\frac{5π}{4}+2kπ≤2x+\frac{π}{3}≤\frac{π}{4}+2kπ,k∈Z$,
∴$-\frac{19π}{12}+2kπ≤2x≤-\frac{π}{12}+2kπ,k∈Z$,
可得:$-\frac{19π}{24}+kπ≤x≤-\frac{π}{24}+kπ,k∈Z$,
不等式f(x)≤1的解集为$\{x|-\frac{19π}{24}+kπ≤x≤-\frac{π}{24}+kπ,k∈Z\}$.…(12分)
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,考查了正弦函数的图象和性质,考查了学生基础知识的运用和图象观察能力,属于基本知识的考查.

| A. | -16 | B. | -4 | C. | 4 | D. | -4或4 |
| A. | 向左平移1个单位 | B. | 向右平移1个单位 | ||
| C. | 向左平移$\frac{1}{2}$个单位 | D. | 向右平移$\frac{1}{2}$个单位 |