题目内容
9.已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=3,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{13}$.(1)求|$\overrightarrow{b}$|;
(2)求2$\overrightarrow{a}$-$\overrightarrow{b}$在$\overrightarrow{b}$方向上的投影.
分析 (1)把|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{13}$两边平方可得|$\overrightarrow{b}$|的方程,解方程可得;
(2)由(1)可得(2$\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{b}$的值,而2$\overrightarrow{a}$-$\overrightarrow{b}$在$\overrightarrow{b}$方向上的投影为$\frac{(2\overrightarrow{a}-\overrightarrow{b})•\overrightarrow{b}}{|\overrightarrow{b}|}$,代值计算可得.
解答 解:(1)∵向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=3,|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{13}$,
∴($\overrightarrow{a}$+$\overrightarrow{b}$)2=13,∴9+2×$3×|\overrightarrow{b}|$×cos120°+|$\overrightarrow{b}$|2=13,
整理可得|$\overrightarrow{b}$|2-3|$\overrightarrow{b}$|-4=0,
解得|$\overrightarrow{b}$|=4,或|$\overrightarrow{b}$|=-1(舍去);
(2)由(1)可得(2$\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{b}$=2$\overrightarrow{a}$•$\overrightarrow{b}$-${\overrightarrow{b}}^{2}$
=2×$3×4×(-\frac{1}{2})$-16=-28,
∴2$\overrightarrow{a}$-$\overrightarrow{b}$在$\overrightarrow{b}$方向上的投影为|2$\overrightarrow{a}$-$\overrightarrow{b}$|cos<2$\overrightarrow{a}$-$\overrightarrow{b}$,$\overrightarrow{b}$>
=$\frac{(2\overrightarrow{a}-\overrightarrow{b})•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{-28}{4}$=-7.
点评 本题考查向量的投影,涉及向量的数量积和模长公式,属中档题.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案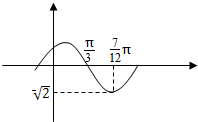 函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,
函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,(1)求函数f(x)的解析式;
(2)解不等式f(x)≤1.
| A. | [1,4] | B. | [0,$\frac{4}{3}$] | C. | [0,$\frac{1}{2}$] | D. | (-∞,0]∪($\frac{4}{3}$,+∞] |