题目内容
设 ,
, 且
且 ,其中当
,其中当 为偶数时,
为偶数时,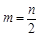 ;当
;当 为奇数时,
为奇数时, .
.
(1)证明:当 ,
, 时,
时, ;
;
(2)记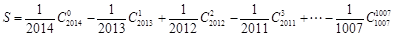 ,求
,求 的值.
的值.
(1)证明见解析;(2)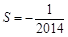
解析试题分析:(1)从题设可以看出本题要分类,按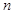 的奇偶性来分类,如当
的奇偶性来分类,如当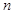 为奇数时,
为奇数时,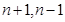 都是偶数,
都是偶数,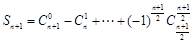 ,
,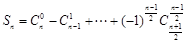 ,
,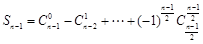 ,
,
通过计算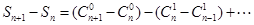 ,应用公式
,应用公式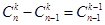 可得结论,当然
可得结论,当然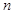 为偶数时也同样证明;(2)待求式子比较难,
为偶数时也同样证明;(2)待求式子比较难,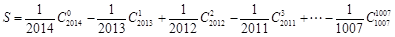 ,
,
把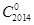 的系数变为1,有
的系数变为1,有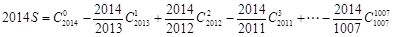
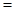
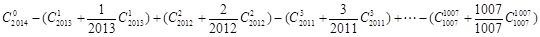
由公式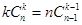 ,上式可变为
,上式可变为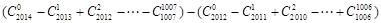
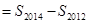 ,而由(1)可得数列
,而由(1)可得数列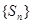 是周期为6的周期数列,故
是周期为6的周期数列,故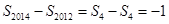 ,从而计算得
,从而计算得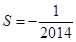 .
.
试题解析:(1)当 为奇数时,
为奇数时,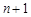 为偶数,
为偶数,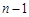 为偶数,
为偶数,
∵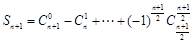 ,
,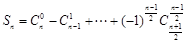 ,
,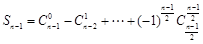 ,
,
∴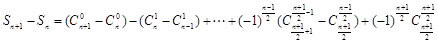
=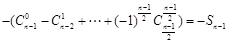 .
.
∴当 为奇数时,
为奇数时, 成立. 5分
成立. 5分
同理可证,当 为偶数时,
为偶数时, 也成立. 6分
也成立. 6分
(2)由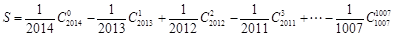 ,得
,得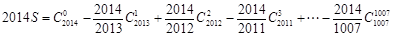
=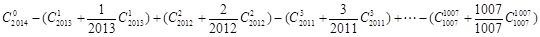
=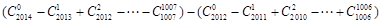
=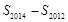 . 9分
. 9分
又由 ,得
,得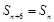 ,所以
,所以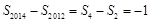 ,
,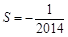 . 10分
. 10分
考点:组合数的性质,周期数列

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 的展开式中前三项的系数成等差数列.设
的展开式中前三项的系数成等差数列.设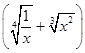 n展开式中的倒数第三项的系数为45,求:
n展开式中的倒数第三项的系数为45,求: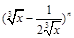 的展开式中,第6项
的展开式中,第6项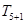 为常数项.
为常数项. 的展开式中x2项的系数为60,则实数a=
的展开式中x2项的系数为60,则实数a=