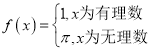题目内容
【题目】选修4-4：坐标系与参数方程
在极坐标系中，曲线
的极坐标方程为
,以坐标原点
为极点，以
轴正半轴为极轴，建立极坐标系，直线
的参数方程为
（t为参数).
（1）写出曲线的参数方程和直线的普通方程；
（2）已知点
是曲线上一点，，求点到直线的最小距离.
【答案】(1) 
,（
为参数）
(2) 
【解析】
试题分析：（1）根据
，把曲线
的极坐标方程转化为直角坐标方程，进而得到曲线的参数方程；根据代入消参法，把直线
的参数方程转化为普通方程；
（2）设曲线上任意一点
为
，则点到直线的距离
，
利用余弦型函数的有界性求最值即可.
试题解析：
(1)由曲线的极坐标方程得： 
，∴曲线的直角坐标方程为: 
，
曲线的参数方程为,（为参数）；直线的普通方程为： 
.
(2)设曲线上任意一点为，则
点到直线的距离为
.
练习册系列答案
相关题目
【题目】基于移动互联技术的共享单车被称为“新四大发明”之一,短时间内就风靡全国,带给人们新的出行体验.某共享单车运营公司的市场研究人员为了解公司的经营状况,对该公司最近六个月内的市场占有率进行了统计,结果如下表:
月份 | 2017.8 | 2017.9 | 2017.10 | 2017.11 | 2017.12 | 2018.1 |
月份代码x | 1 | 2 | 3 | 4 | 5 | 6 |
市 场占有率y(%) | 11 | 13 | 16 | 15 | 20 | 21 |
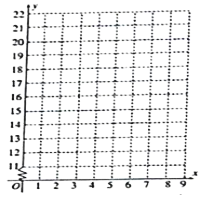
(1)请在给出的坐标纸中作出散点图;
(2)求y关于x的线性回归方程,并预测该公司2018年2月份的市场占有率;
参考公式:回归直线方程为
其中: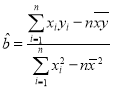
,
