题目内容
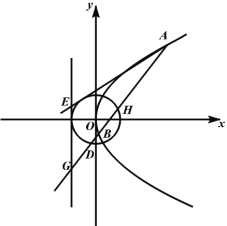
【题目】以平面直角坐标系的原点
为极点，
轴的正半轴为极轴，建立极坐标系，曲线
的极坐标方程为
，将曲线绕极点逆时针旋转
后得到曲线
.
（Ⅰ）求曲线的极坐标方程；
（Ⅱ）若直线
：
与，分别相交于异于极点的
，
两点，求
的最大值.
【答案】（Ⅰ）
；（Ⅱ）
.
【解析】
（Ⅰ）设
上任意一点的极坐标为
，结合条件可知
在
上，再代入的极坐标方程
，即可得出的极坐标方程；
（Ⅱ）根据题意，设
，
，利用极径的几何意义得出
，再根据三角函数关系式的恒等变换及正弦型函数的性质，即可求出结果．
解：（Ⅰ）设上任意一点的极坐标为，
由于曲线绕极点逆时针旋转
后得到曲线，
则在上，
而曲线的极坐标方程为，
所以，
故曲线的极坐标方程为.
（Ⅱ）根据题意，可设，，
，
当且仅当
时等号成立，
故
的最大值为.
练习册系列答案
阅读快车系列答案
相关题目
【题目】如果某企业每月生猪的死亡率不超过百分之一，则该企业考核为优秀.现获得某企业2019年1月到8月的相关数据如下表所示：
月份 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 |
月养殖量/千只 | 3 | 4 | 5 | 6 | 7 | 9 | 10 | 12 |
月利润/十万元 | 3.6 | 4.1 | 4.4 | 5.2 | 6.2 | 7.5 | 7.9 | 9.1 |
生猪死亡数最/只 | 29 | 37 | 49 | 53 | 77 | 98 | 126 | 145 |
（1）求出月利润；y（十万元）关于月养殖量x（千只）的线性回归方程（精确到0.01）；
（2）若2019年9月份该企业月养殖量为1.4万只，请你预估该月月利润是多少万元；
（3）从该企业2019年1月到8月这8个月中任意选取3个月，用X表示3个月中该企业考核获得优秀的个数，求X的分布列和数学期望./p>
参考数据：
，
，
，
附：线性回归方程
中，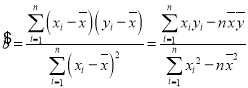
，
