题目内容
【题目】如图，AB为圆O的直径，点E，F在圆O上，且AB//EF，AB=2EF，矩形ABCD所在的平面和圆O所在的平面互相垂直.
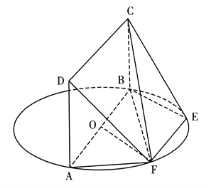
（I）证明：OF／／平面BEC；
（Ⅱ）证明：平面ADF
平面BCF．
【答案】（Ⅰ）（Ⅱ）详见解析.
【解析】
试题分析：（Ⅰ）要证明线面平行，需先证明线线平行，根据梯形
内的线线关系可得
,这样根据线面平行的判定定理，可得线面平行；（Ⅱ）要证明面面垂直，需先证明线面垂直，而要证明线面垂直，需先证明线线垂直，即证明
和
，这样就可证明
平面
，最后证明证明得到面面垂直.
试题解析：证明：（Ⅰ）
为圆
的直径，
，
，
,
四边形
为平行四边形，
，
又
平面
，
平面,
平面.
（Ⅱ）
四边形
为矩形，
，
又
平面与圆
所在平面垂直，且交线为
，
平面
，
平面，
，
又为圆
的直径，
，
又
,
平面,
又平面
,
平面
平面.
练习册系列答案
相关题目
