Question

【题目】已知三次函数，

（1）若函数过点且在点处的切线方程是，求函数的解析式；

（2）在（1）的条件下，若对于区间上任意两个自变量的值，

都有，求实数的最小值．

Answer 1

【答案】（1）;（2）t的最小值是20.

【解析】试题分析：（1）把 代入 的解析式，再根据，得到关于 及 的三元一次方程组，求出方程组的解即可得到 及 的值，进而得到的解析式；（2）把（1）求出 及 的值代入导函数中确定出导函数的解析式，令导函数对于求出 的值，然后分别求出的及闭区间的端点时的函数值，得到的最大值和最小值，求出最大值和最小值的差即为 的最大值，让 大于等于求出的最大值即可得到的取值范围.

试题解析：（1）函数过点，

又，函数在点处的切线方程是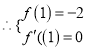， ， 解得，故

（2）由（1）知，令解得，

， 在区间上，

对于区间上任意两个自变量的值，都有，

,所以t的最小值是20