题目内容
如图椭圆C的方程为
+
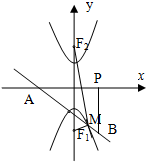
=1(a>b>0),A是椭圆C的短轴左顶点,过A点作斜率为-1的直线交椭圆于B点,点P(1,0),且BP∥y轴,△APB的面积为
.
(1)求椭圆C的方程;
(2)在直线AB上求一点M,使得以椭圆C的焦点为焦点,且过M的双曲线E的实轴最长,并求此双曲线E的方程.

| y2 |
| a2 |
| x2 |
| b2 |
| 9 |
| 2 |
(1)求椭圆C的方程;
(2)在直线AB上求一点M,使得以椭圆C的焦点为焦点,且过M的双曲线E的实轴最长,并求此双曲线E的方程.

(1)S△APB=
AP•PB=
,又∠PAB=45°,AP=PB,故AP=BP=3.
∵P(1,0),A(-2,0),B(1,-3)
∴b=2,将B(1,-3)代入椭圆得:
得a2=12,
所求椭圆方程为
+
=1.
(2)设椭圆C的焦点为F1,F2,
则易知F1(0,-2
)F2(0,2
),
直线AB的方程为:x+y+2=0,因为M在双曲线E上,要双曲线E的实轴最大,只须||MF1|-|MF2||最大,设F1(0,-2
)关于直线AB的对称点为F1'(2
-2,-2),则直线F2F1′与直线的交点为所求M,
因为F2F1′的方程为:y+(3+2
)x-2
=0,联立
得M(1,-3)
又2a′=||MF1|-|MF2||=||MF1'|-|MF2||≤|F2F1'|
=
=2
,故
=
,b′=
,
故所求双曲线方程为:
-
=1
| 1 |
| 2 |
| 9 |
| 2 |
∵P(1,0),A(-2,0),B(1,-3)
∴b=2,将B(1,-3)代入椭圆得:
|
所求椭圆方程为
| y2 |
| 12 |
| x2 |
| 4 |
(2)设椭圆C的焦点为F1,F2,
则易知F1(0,-2
| 2 |
| 2 |
直线AB的方程为:x+y+2=0,因为M在双曲线E上,要双曲线E的实轴最大,只须||MF1|-|MF2||最大,设F1(0,-2
| 2 |
| 2 |
因为F2F1′的方程为:y+(3+2
| 2 |
| 2 |
|
又2a′=||MF1|-|MF2||=||MF1'|-|MF2||≤|F2F1'|
=
(2
|
| 6 |
| a | ′max |
| 6 |
| 2 |
故所求双曲线方程为:
| y2 |
| 6 |
| x2 |
| 2 |


练习册系列答案
相关题目

 是圆
是圆 的直径,
的直径, 是圆
是圆 的切线,切点为
的切线,切点为 ,
, 平行于弦
平行于弦 ,若
,若 ,
, ,则
,则 .
.