题目内容

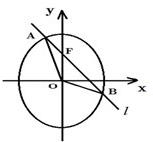
已知椭圆
x2
3
+
y2
2
=1，F是右焦点，若直线L过F与椭圆相交于A，B两点，且
AF
=2
FB
，则直线L的方程为：______．
椭圆
x2
3
+
y2
2
=1的右焦点F（1，0），右准线方程为x=3
设直线L的方程为y=k（x-1），代入椭圆方程消y可得（2+3k2）x2-6k2x+3k2-6=0
设A（x1，y1），B（x2，y2），则x1+x2=
6k2
2+3k2
①，x1x2=
3k2-6
2+3k2
②，
∵
AF
=2
FB
，∴3-x1=2（3-x2）③
联立①②③可得k=±
2
，
∴直线L的方程为y=±
2
(x-1)．
故答案为：y=±
2
(x-1)．
练习册系列答案
相关题目
已知椭圆C的中心在原点，一个焦点为F(0，
2
)，且长轴长与短轴长的比为
2
：1．
（1）求椭圆C的方程；
（2）若椭圆C上在第一象限内的一点P的横坐标为1，过点P作倾斜角互补的两条不同的直线PA，PB分别交椭圆C于另外两点A，B．求证：直线AB的斜率为定值．
已知O为坐标原点，F为椭圆C：x2+
y2
2
=1在y轴正半轴上的焦点，过F且斜率为-
2
的直线l与C交于A、B两点，点P满足
OA
+
OB
+
OP
=
0
．
（Ⅰ）证明：点P在C上；
（Ⅱ）设点P关于点O的对称点为Q，证明：A、P、B、Q四点在同一圆上．
直线l过x轴上的点M，l交椭圆
x2
8
+
y2
4
=1于A，B两点，O是坐标原点．
（1）若M的坐标为（2，0），当OA⊥OB时，求直线l的方程；
（2）若M的坐标为（1，0），设直线l的斜率为k（k≠0），是否存直线l，使得l垂直平分椭圆的一条弦？如果存在，求k的取值范围；如果不存在，说明理由．
已知椭圆C的中心在原点，焦点在x轴上，离心率e=
1
2
，一个顶点的坐标为(0，
3
)．
（1）求椭圆C的方程；
（2）椭圆C的左焦点为F，右顶点为A，直线l：y=kx+m与椭圆C相交于M，N两点且
AM
•
AN
=0，试问：是否存在实数λ，使得S△FMN=λS△AMN成立，若存在，求出λ的值；若不存在，请说明理由．
若直线y=kx+2与曲线y=
x2-1
，|x|＞1
1-x2
，|x|≤1
恰有两个不同的交点，则k∈______．
已知椭圆C1：
x2
4
+y2=1，椭圆C2以C1的长轴为短轴，且与C1有相同的离心率．
（1）求椭圆C2的方程；
（2）设O为坐标原点，点A，B分别在椭圆C1和C2上，
OB
=2
OA
，求直线AB的方程．
将曲线C1：(x-4)2+y2=4所有点的横坐标不变，纵坐标变为原来的
1
2
得到曲线C2，将曲线C2向左（x轴负方向）平移4个单位，得到曲线C3．
（Ⅰ）求曲线C3的方程；
（Ⅱ）垂直于x轴的直线l与曲线C3相交于C、D两点（C、D可以重合），已知A（-2，0），B（2，0），直线AC、BD相交于点P，求P点的轨迹方程．
如图椭圆C的方程为
y2
a2
+
x2
b2
=1(a＞b＞0)，A是椭圆C的短轴左顶点，过A点作斜率为-1的直线交椭圆于B点，点P（1，0），且BP∥y轴，△APB的面积为
9
2
．
（1）求椭圆C的方程；
（2）在直线AB上求一点M，使得以椭圆C的焦点为焦点，且过M的双曲线E的实轴最长，并求此双曲线E的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网