题目内容
【题目】已知:以点![]() (
(![]() )为圆心的圆与
)为圆心的圆与![]() 轴交
轴交
于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线![]() 与圆C交于点M, N,若OM = ON,求圆C的方程.
与圆C交于点M, N,若OM = ON,求圆C的方程.
【答案】(1)根据条件写成圆的方程,求出点A,B的坐标,进而写出△OAB的面积即可得证;
(2)![]()
【解析】试题分析:(1)设出圆C的方程,求得A、B的坐标,再根据S△AOB=![]() OAOB,计算可得结论.
OAOB,计算可得结论.
(2)设MN的中点为H,则CH⊥MN,根据C、H、O三点共线,KMN=﹣2,由直线OC的斜率![]() ,求得t的值,可得所求的圆C的方程.
,求得t的值,可得所求的圆C的方程.
试题解析:
(1)![]() ,
,![]() .
.
设圆![]() 的方程是
的方程是 ![]()
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]()
![]() ,即:
,即:![]() 的面积为定值.
的面积为定值.
(2)![]()
![]() 垂直平分线段
垂直平分线段![]() .
.
![]() ,
,![]() 直线
直线![]() 的方程是
的方程是![]() .
.
![]() ,解得:
,解得:![]()
当![]() 时,圆心
时,圆心![]() 的坐标为
的坐标为![]() ,
,![]() ,此时
,此时![]() 到直线
到直线![]() 的距离
的距离![]() ,圆
,圆![]() 与直线
与直线![]() 相交于两点.
相交于两点.
当![]() 时,圆心
时,圆心![]() 的坐标为
的坐标为![]() ,
,![]() ,此时
,此时![]() 到直线
到直线![]() 的距离
的距离![]() 圆
圆![]() 与直线
与直线![]() 不相交,
不相交,![]() 不符合题意舍去.
不符合题意舍去.
![]() 圆
圆![]() 的方程为
的方程为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
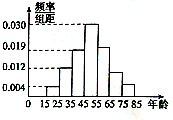
【题目】某单位每天的用电量![]() (度)与当天最高气温
(度)与当天最高气温![]() (℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
(℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
最高气温(℃) | 26 | 29 | 31 | 34 |
用电量 (度) | 22 | 26 | 34 | 38 |
(Ⅰ)根据表中数据,求出回归直线的方程![]() (其中
(其中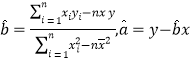 );
);
(Ⅱ)试预测某天最高气温为33℃时,该单位当天的用电量(精确到1度).