题目内容
【题目】已知函数 ![]() .
.
(1)若 ![]() ,求函数y=f(x)的单调区间;
,求函数y=f(x)的单调区间;
(2)若x=﹣1是函数y=f(x)的一个极值点,试判断此时函数y=f(x)的零点个数,并说明理由.
【答案】
(1)解:f'(x)=x2﹣2bx+2.
![]() 时,f'(x)=x2﹣3x+2=(x﹣1)(x﹣2),
时,f'(x)=x2﹣3x+2=(x﹣1)(x﹣2),
令f'(x)>0解得x<1或x>2.
所以, ![]() 时函数的单调递增区间为(﹣∞,1),(2,+∞).
时函数的单调递增区间为(﹣∞,1),(2,+∞).
令f'(x)<0解得1<x<2.
所以, ![]() 时函数的单调递减区间为(1,2)
时函数的单调递减区间为(1,2)
(2)解:因为x=﹣1是函数y=f(x)的一个极值点,
则f'(﹣1)=0,故:1+2b+2=0解得: ![]() ,
,
此时f'(x)=x2﹣2bx+2=x2+3x+2,
令f'(x)=0解得:x=﹣2或x=﹣1.
则x变化时,f'(x),f(x)的变化情况如下.
x | (﹣∞,﹣2) | ﹣2 | (﹣2,﹣1) | ﹣1 | (﹣1,+∞) |
f'(x) | + | 0 | ﹣ | 0 | + |
f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
故此时x=﹣1时,f(x)有极小值 ![]() ;
;
x=﹣2时,f(x)有极大值 ![]() ;
;
则当x>﹣2时,f(x)≥f(﹣1)>0,显然函数在(﹣2,+∞)上无零点.
又 ![]() ,(也可取x=﹣4等),则f(﹣3)f(﹣2)<0,
,(也可取x=﹣4等),则f(﹣3)f(﹣2)<0,
结合函数在(﹣∞,﹣2)上单调递增,故由零点存在定理知,函数在(﹣∞,﹣2)上必有唯一零点.
综上:若x=﹣1是函数y=f(x)的一个极值点,则此时函数y=f(x)在R上有唯一零点
【解析】(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(2)根据x=﹣1是函数y=f(x)的一个极值点,求出b的值,求出函数的导数,解关于导函数的方程,求出函数的单调区间,从而判断函数的零点个数即可.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的极值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.

【题目】某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限x年 | 3 | 5 | 6 | 7 | 9 |
年推销金额y万元 | 2 | 3 | 3 | 4 | 5 |
(1)从编号1﹣5的五位推销员中随机取出两位,求他们年推销金额之和不少于7万元的概率;
(2)求年推销金额y关于工作年限x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;若第6名产品推销员的工作年限为11年,试估计他的年推销金额. 附:回归直线的斜率和截距的最小二乘法估计公式为:
;若第6名产品推销员的工作年限为11年,试估计他的年推销金额. 附:回归直线的斜率和截距的最小二乘法估计公式为: ![]() =
= 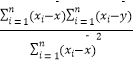 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.