题目内容
【题目】如图,在三棱锥S﹣ABC中,△ABC为直角三角形,且∠ACB=90°,SA⊥平面ABC,AD⊥SC.
求证:AD⊥平面SBC.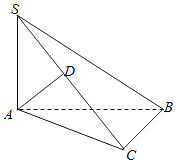
【答案】证明:∵∠ACB=90°,∴BC⊥AC.
又SA⊥面ABC,∴SA⊥BC,
∴BC⊥面SAC,∴BC⊥AD.
又SC⊥AD,SC∩BC=C,
∴AD⊥面SBC.
【解析】由已知可得BC⊥AC,再根据线面垂直的性质定理可得到SA⊥BC,然后根据线面垂直的判定定理可得BC⊥面SAC进而得到BC⊥AD,再根据线面垂直的性质定理可得到结论。
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目