题目内容
【题目】如图,三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是 ![]() ,D是AC的中点.
,D是AC的中点.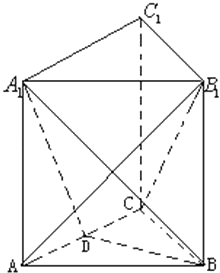
(1)求证:B1C∥平面A1BD;
(2)求二面角A1﹣BD﹣A的大小;
(3)求直线AB1与平面A1BD所成的角的正弦值.
【答案】
(1)解:设AB1与A1B相交于点P,连接PD,则P为AB1中点,
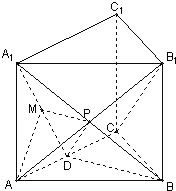
∵D为AC中点,∴PD∥B1C.
又∵PD平面A1BD,B1C平面A1BD
∴B1C∥平面A1BD.
(2)解:∵正三棱住ABC﹣A1B1C1,
∴AA1⊥底面ABC.
又∵BD⊥AC
∴A1D⊥BD
∴∠A1DA就是二面角A1﹣BD﹣A的平面角.
∵AA1= ![]() ,AD=
,AD= ![]() AC=1
AC=1
∴tan∠A1DA= ![]()
∴∠A1DA= ![]() ,即二面角A1﹣BD﹣A的大小是
,即二面角A1﹣BD﹣A的大小是 ![]() .
.
(3)解:由(2)作AM⊥A1D,M为垂足.
∵BD⊥AC,平面A1ACC1⊥平面ABC,平面A1ACC1∩平面ABC=AC
∴BD⊥平面A1ACC1,
∵AM平面A1ACC1,
∴BD⊥AM
∵A1D∩BD=D
∴AM⊥平面A1DB,连接MP,则∠APM就是直线A1B与平面A1BD所成的角.
∵AA1= ![]() ,AD=1,∴在Rt△AA1D中,∠A1DA=
,AD=1,∴在Rt△AA1D中,∠A1DA= ![]() ,
,
∴AM=1×sin60°= ![]() ,AP=AB1=
,AP=AB1= ![]() .
.
∴sin∠APM= 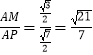
∴直线AB1与平面A1BD所成的角的正弦值为 ![]() .
.
【解析】(1)设AB1与A1B相交于点P,连接PD,则P为AB1中点,D是AC的中点,根据中位线定理不难得出PD∥B1C,则B1C∥平面A1BD,(2)根据正三棱柱的性质可得出AA1⊥底面ABC,又因为BD⊥AC,由三垂线定理可得出∠A1DA就是二面角A1﹣BD﹣A的平面角,在三角形A1DA中进行求解即可,(3)由(2)作AM⊥A1D,M为垂足,不难证出∠APM就是直线A1B与平面A1BD所成的角,在三角形APM进行求解即可、
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则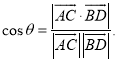 .
.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案