题目内容
(本题满分14分)设函数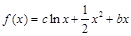
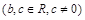 ,且
,且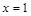 为
为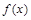 的极值点.
的极值点.
(Ⅰ) 若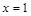 为
为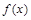 的极大值点,求
的极大值点,求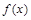 的单调区间(用
的单调区间(用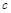 表示);
表示);
(Ⅱ) 若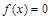 恰有两解,求实数
恰有两解,求实数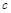 的取值范围.
的取值范围.
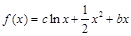
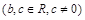 ,且
,且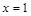 为
为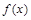 的极值点.
的极值点.(Ⅰ) 若
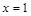 为
为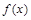 的极大值点,求
的极大值点,求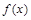 的单调区间(用
的单调区间(用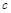 表示);
表示);(Ⅱ) 若
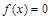 恰有两解,求实数
恰有两解,求实数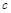 的取值范围.
的取值范围.试题分析:解:
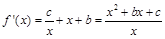 ,又
,又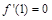 ,则
,则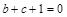 ,
,所以
 且
且 , 3分
, 3分(Ⅰ)因为
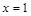 为
为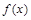 的极大值点,所以
的极大值点,所以 .
. 令
 ,得
,得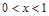 或
或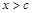 ;令
;令 ,得
,得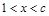 .
. 所以
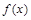 的递增区间为
的递增区间为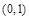 ,
,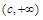 ;递减区间为
;递减区间为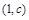 . 6分
. 6分(Ⅱ)①若
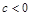 ,则
,则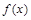 在
在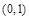 上递减,在
上递减,在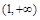 上递增.
上递增. 若
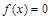 恰有两解,则
恰有两解,则 ,即
,即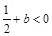 ,所以
,所以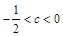 . 8分
. 8分②若
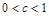 ,则
,则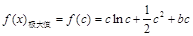 ,
, .
. 因为
 ,则
,则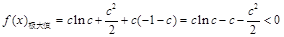 ,
,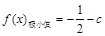 ,从而
,从而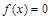 只有一解; 10分
只有一解; 10分③若
 ,则
,则 ,
,从而
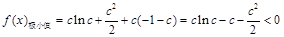 ,
,则
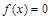 只有一解. 12分
只有一解. 12分综上,使
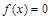 恰有两解的
恰有两解的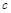 的范围为
的范围为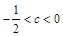 14分
14分点评:

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
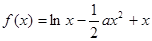
 时,求
时,求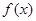 的最大值;
的最大值;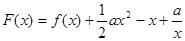
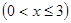 ,以其图象上任意一点
,以其图象上任意一点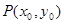 为切点的切线的斜率
为切点的切线的斜率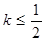 恒成立,求实数
恒成立,求实数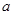 的取值范围;
的取值范围;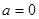 时,方程
时,方程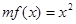 有唯一实数解,求正数
有唯一实数解,求正数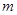 的值.
的值.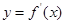 的图象,则下列命题错误的是( )
的图象,则下列命题错误的是( )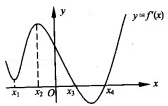
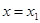 处有极小值
处有极小值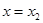 处有极大值
处有极大值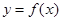 在
在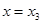 处有极小值
处有极小值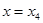 处有极小值
处有极小值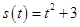 (
(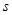 单位:
单位: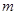 ,
,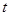 单位:
单位: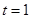 时的瞬时速度为( )
时的瞬时速度为( )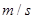
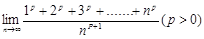 表示成定积分( )
表示成定积分( )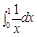
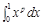
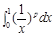
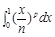
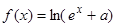 是实数集R上的奇函数,且
是实数集R上的奇函数,且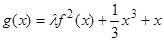 在R上为增函数。
在R上为增函数。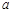 的值;
的值;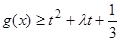 在
在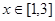 恒成立时的实数t的取值范围。
恒成立时的实数t的取值范围。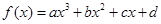 (
(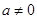 ),定义:设f″(x)是函数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数
),定义:设f″(x)是函数y=f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数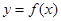 的“拐点”.有同学发现:“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,若函数
的“拐点”.有同学发现:“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,若函数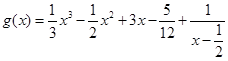 ,则
,则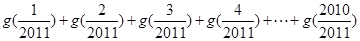 =( )
=( )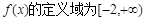 ,且
,且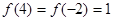 ,
,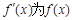 的导函数,函数
的导函数,函数 的图象如图所示.则平面区域
的图象如图所示.则平面区域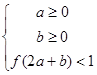 所围成的面积是( )
所围成的面积是( )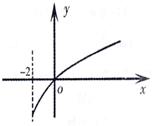
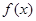 ,恒有
,恒有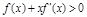 ,则
,则