题目内容
(本小题满分12分)
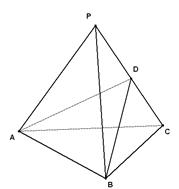
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,
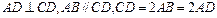 .
.

(Ⅰ)求证: ;
;
(Ⅱ)在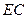 上找一点
上找一点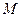 ,使得
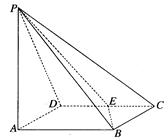
,使得 平面
平面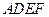 ,请确定
,请确定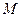 点的位置,并给出证明.
点的位置,并给出证明.
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,
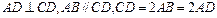 .
.
(Ⅰ)求证:
 ;
;(Ⅱ)在
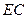 上找一点
上找一点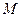 ,使得
,使得 平面
平面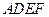 ,请确定
,请确定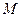 点的位置,并给出证明.
点的位置,并给出证明. 证明:(Ⅰ)因为正方形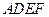 与梯形
与梯形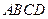 所在的平面互相垂直,
所在的平面互相垂直,
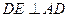
所以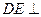 平面
平面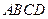
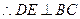 ………………1分
………………1分
因为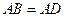 ,所以
,所以
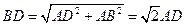
取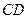 中点
中点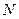 ,连接
,连接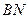
则由题意知:四边形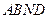 为正方形
为正方形
所以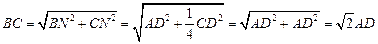 ,
,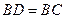
则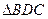 为等腰直角三角形
为等腰直角三角形
则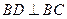 …………5分
…………5分
则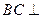 平面
平面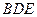
则 ………………7分
………………7分
(Ⅱ)取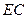 中点
中点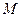 ,则有
,则有
 平面
平面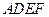 …………8分
…………8分
证明如下:连接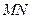
由(Ⅰ)知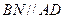 ,
,
所以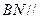 平面
平面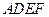
又因为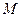 、
、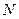 分别为
分别为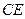 、
、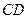 的中点,所以
的中点,所以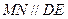
则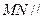 平面
平面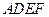 ………………10分
………………10分
则平面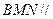 平面
平面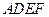 ,所以
,所以 平面
平面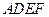 ……………………12分
……………………12分
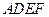 与梯形
与梯形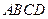 所在的平面互相垂直,
所在的平面互相垂直,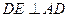
所以
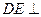 平面
平面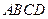
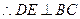 ………………1分
………………1分因为
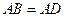 ,所以
,所以
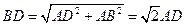
取
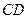 中点
中点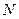 ,连接
,连接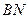
则由题意知:四边形
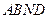 为正方形
为正方形所以
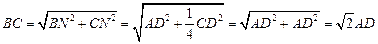 ,
,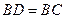
则
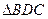 为等腰直角三角形
为等腰直角三角形则
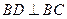 …………5分
…………5分则
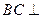 平面
平面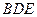
则
 ………………7分
………………7分(Ⅱ)取
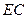 中点
中点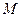 ,则有
,则有 平面
平面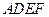 …………8分
…………8分证明如下:连接
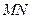
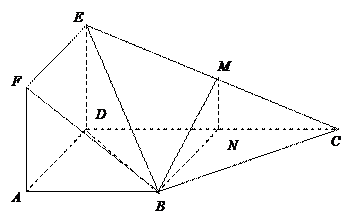
由(Ⅰ)知
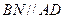 ,
,所以
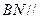 平面
平面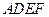
又因为
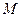 、
、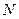 分别为
分别为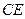 、
、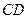 的中点,所以
的中点,所以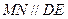
则
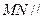 平面
平面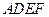 ………………10分
………………10分则平面
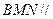 平面
平面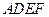 ,所以
,所以 平面
平面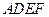 ……………………12分
……………………12分略

练习册系列答案
相关题目
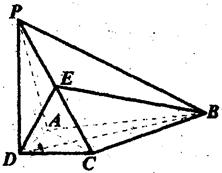
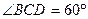 ,E是CD的中点,
,E是CD的中点,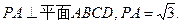
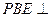 平面PAB;
平面PAB; 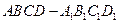 中,
中,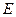 、
、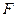 分别为
分别为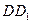 、
、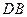 的
的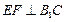 ;
;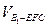 的体积.
的体积.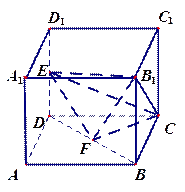
 E为PC的中点,AD=CD=l,BC=PC,
E为PC的中点,AD=CD=l,BC=PC,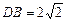
 杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由。
杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由。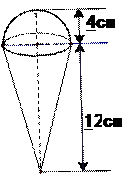
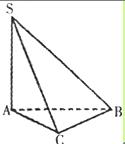
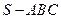 中,
中,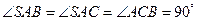 ,且
,且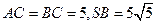 。
。
 ;
;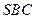 与底面
与底面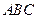 所成二面角的大小;
所成二面角的大小;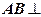 平面
平面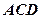 ,
,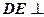 平面
平面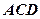 ,
,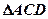 为
为 等边三角形,
等边三角形,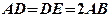 ,
, 为
为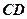 中点.
中点.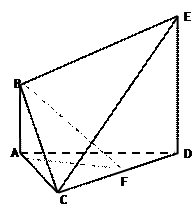
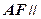 平面
平面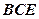 ;
;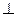 平面
平面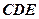 ;
;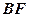 与平面
与平面
 的正弦值.
的正弦值.