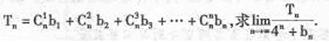题目内容
(本小题共13分)在等差数列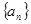 中,
中,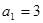 ,其前
,其前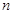 项和为
项和为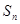 ,等比数列
,等比数列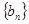 的各项均为正数,
的各项均为正数,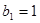 ,公比为
,公比为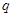 ,且
,且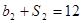 ,
, 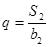 .
.
(Ⅰ)求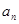 与
与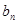 ;
;
(Ⅱ)证明: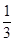 ≤
≤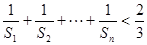 .
.
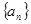 中,
中,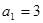 ,其前
,其前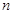 项和为
项和为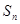 ,等比数列
,等比数列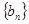 的各项均为正数,
的各项均为正数,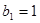 ,公比为
,公比为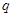 ,且
,且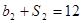 ,
, 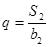 .
.(Ⅰ)求
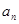 与
与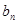 ;
;(Ⅱ)证明:
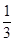 ≤
≤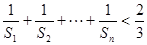 .
.解:(Ⅰ)设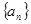 的公差为
的公差为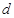 ,
,
因为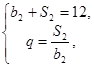 所以
所以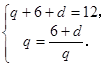
解得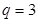 或
或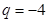 (舍),
(舍),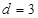 .
.
故 ,
,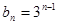 . ……………6分
. ……………6分
(Ⅱ)因为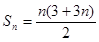 ,
,
所以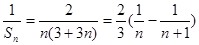 . ………9分
. ………9分
故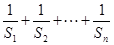
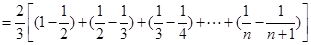
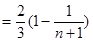 . ………11分
. ………11分
因为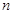 ≥
≥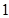 ,所以
,所以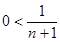 ≤
≤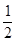 ,于是
,于是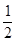 ≤
≤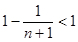 ,
,
所以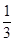 ≤
≤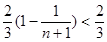 .
.
即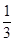 ≤
≤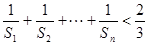 . ……………13分
. ……………13分
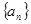 的公差为
的公差为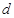 ,
,因为
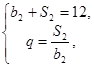 所以
所以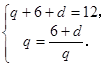
解得
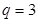 或
或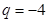 (舍),
(舍),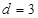 .
.故
 ,
,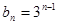 . ……………6分
. ……………6分(Ⅱ)因为
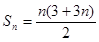 ,
,所以
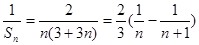 . ………9分
. ………9分故
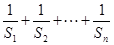
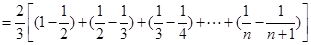
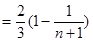 . ………11分
. ………11分因为
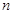 ≥
≥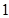 ,所以
,所以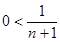 ≤
≤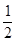 ,于是
,于是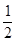 ≤
≤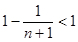 ,
,所以
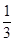 ≤
≤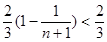 .
.即
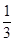 ≤
≤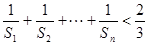 . ……………13分
. ……………13分本题考查等差数列和等比数列的通项公式以及等比数列的前n项和,考查学生利用基本量思想和方程思想的解题能力。清晰数列的通项公式和求和公式联立方程求解是解决本类题目常用的解题思路,考查学生的计算能力。在数列求和问题中,由于题目的千变万化,使得不少同学一筹莫展,方法老师也介绍过,就不清楚什么特征用什么方法.为此提供一个通法 “特征联想法”:就是抓住数列的通项公式的特征,再去联想常用数列的求和方法.通项公式作为数列的灵魂,只有抓住它的特征,才能对号入座,得到求和方法.
特征一: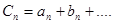 ,数列
,数列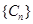 的通项公式能够分解成几部分,一般用“分组求和法”.特征二:
的通项公式能够分解成几部分,一般用“分组求和法”.特征二: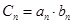 ,数列
,数列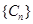 的通项公式能够分解成等差数列和等比数列的乘积,一般用“错位相减法”.特征三:
的通项公式能够分解成等差数列和等比数列的乘积,一般用“错位相减法”.特征三: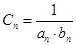 ,数列
,数列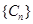 的通项公式是一个分式结构,一般采用“裂项相消法”.特征四:
的通项公式是一个分式结构,一般采用“裂项相消法”.特征四: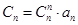 ,数列
,数列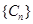 的通项公式是一个组合数和等差数列通项公式组成,一般采用“倒序相加法”.本题第二问采用裂项相消法,结合不等式的放缩法进行证明.
的通项公式是一个组合数和等差数列通项公式组成,一般采用“倒序相加法”.本题第二问采用裂项相消法,结合不等式的放缩法进行证明.
特征一:
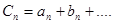 ,数列
,数列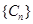 的通项公式能够分解成几部分,一般用“分组求和法”.特征二:
的通项公式能够分解成几部分,一般用“分组求和法”.特征二: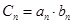 ,数列
,数列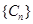 的通项公式能够分解成等差数列和等比数列的乘积,一般用“错位相减法”.特征三:
的通项公式能够分解成等差数列和等比数列的乘积,一般用“错位相减法”.特征三: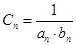 ,数列
,数列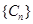 的通项公式是一个分式结构,一般采用“裂项相消法”.特征四:
的通项公式是一个分式结构,一般采用“裂项相消法”.特征四: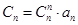 ,数列
,数列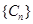 的通项公式是一个组合数和等差数列通项公式组成,一般采用“倒序相加法”.本题第二问采用裂项相消法,结合不等式的放缩法进行证明.
的通项公式是一个组合数和等差数列通项公式组成,一般采用“倒序相加法”.本题第二问采用裂项相消法,结合不等式的放缩法进行证明.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
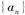 的前n项和为
的前n项和为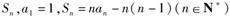 .
.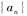 的通项公式;
的通项公式;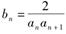 ,求数列
,求数列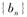 的前n项和Tn
的前n项和Tn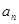 }满足
}满足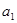 =1,
=1,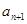 =
=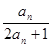 ,(1)计算
,(1)计算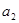 ,
,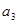 ,
,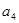 的值;
的值; 的前
的前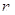 项和为
项和为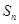 ,且满足
,且满足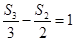 ,则数列
,则数列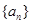 的公差是_________
的公差是_________ }中,
}中,
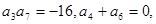 求{
求{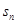 . .
. . 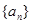 为等差数列,
为等差数列,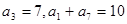 ,
,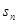 为其前n项和,则使
为其前n项和,则使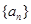 中,
中,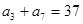 ,则
,则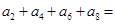 __________。
__________。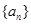 前n项和为
前n项和为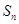 ,已知
,已知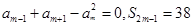
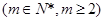 ,则m等于( )
,则m等于( )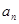 }为等差数列,公差d≠0,同{
}为等差数列,公差d≠0,同{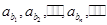 为等比数列,其中
为等比数列,其中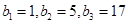 。
。 }的通项公式;
}的通项公式;